题目内容
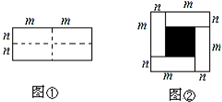
11.图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀分成四块小长方形,然后按图②的形状拼成一个正方形.(1)请和两种不同的方法求图②中阴影部分的面积.
方法1:(m+n)2-4mn 方法2:(m-n)2
(2)观察图②请你写出下列三个代数式;(m+n)2,(m-n)2,mn之间的等量关系;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a-b=3,ab=-2,求:(a+b)2的值;
②已知:a-$\frac{2}{a}$=1,求:a+$\frac{2}{a}$的值.
分析 (1)大正方形的面积减去矩形的面积即可得出阴影部分(小正方形)的面积;
(2)由面积关系容易得出结论;
(3)①根据(2)所得出的关系式,容易求出结果;
②先求出(a+$\frac{2}{a}$)2,即可得出结果.
解答 解:(1)方法1:(m+n)2-4mn,方法2:(m-n)2;
故答案为:(m+n)2-4mn,(m-n)2;
(2)(m+n)2-4mn=(m-n)2;
(3)(a+b)2=(a-b)2+4ab=32+4×(-2)=1;
②∵(a+$\frac{2}{a}$)2=(a-$\frac{2}{a}$)2+4×a×$\frac{2}{a}$=12+8=9,
∴a+$\frac{2}{a}$=±3.
点评 本题考查了完全平方公式的几何背景,正方形和矩形面积的计算;注意仔细观察图形,表示出各图形的面积是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.五一小长假虽只有三天,可美丽竹乡安吉的旅游市场却“火”到不行.记者从安吉县旅游部门获悉,2016年“五一”期间,全县共接待游客64.8万人次,同比增长20.7%.请将64.8万用科学记数法表示( )
| A. | 64.8×104 | B. | 6.48×105 | C. | 0.648×106 | D. | 6.48×106 |
11.小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
| A. | 5x+4(x+2)=44 | B. | 5x+4(x-2)=44 | C. | 9(x+2)=44 | D. | 9(x+2)-4×2=44 |
8.有一个不透明的袋子中装有3个红球、1个白球、1个绿球,这些球只是颜色不同.下列事件中属于确定事件的是( )
| A. | 从袋子中摸出1个球,球的颜色是红色 | |
| B. | 从袋子中摸出2个球,它们的颜色相同 | |
| C. | 从袋子中摸出3个球,有颜色相同的球 | |
| D. | 从袋子中摸出4个球,有颜色相同的球 |
6.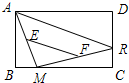 如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
 如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )
如图,矩形ABCD中,点R沿CD边从点C向点D运动,点M在BC边上运动,E、F分别是AM、MR的中点,则EF的长度随着点M、点R的运动( )| A. | 变短 | B. | 变长 | C. | 不变 | D. | 无法确定 |
16.从1-9这九个自然数中任取一个,是2的倍数的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{9}$ |
20.下列各式中是二元一次方程的是( )
| A. | x+π=4 | B. | 2x-y | C. | 3x+y=0 | D. | 2x-5=y2 |
1.已知:最简二次根式$\sqrt{5a-1}$与$\sqrt{10a-16}$能合并,则a的值是( )
| A. | 2 | B. | -2 | C. | 3 | D. | 4.5 |
 如图,△ABC中,D、E分别是AB、AC边的中点,且DE=7cm,则BC=14 cm.
如图,△ABC中,D、E分别是AB、AC边的中点,且DE=7cm,则BC=14 cm.