题目内容

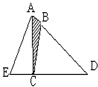如图，AB= $数学公式$ AD，EC= $数学公式$ ED，图中阴影部分与空白部分面积的比________．

1：7
分析：因为AB= $\text{[math]}$ AD，EC= $\text{[math]}$ ED，根据高一定时，三角形的面积与底成正比例的性质可得：阴影部分的面积= $\text{[math]}$ 三角形ACD的面积；三角形ACD的面积= $\text{[math]}$ 三角形ABC的面积，由此可得：阴影部分的面积= $\text{[math]}$ × $\text{[math]}$ 三角形ABC的面积= $\text{[math]}$ 三角形ABC的面积，由此即可解答．
解答：因为AB= $\text{[math]}$ AD，EC= $\text{[math]}$ ED，
所以阴影部分的面积= $\text{[math]}$ 三角形ACD的面积；
三角形ACD的面积= $\text{[math]}$ 三角形ABC的面积，
所以阴影部分的面积= $\text{[math]}$ × $\text{[math]}$ 三角形ABC的面积= $\text{[math]}$ 三角形ABC的面积，
所以阴影部分的面积：空白处的面积=1：7．
故答案为：1：7．
点评：此题考查了高一定时，三角形的面积与底成正比例的性质的灵活应用．

练习册系列答案

综合自测系列答案

走进重高培优测试系列答案

中考全程突破系列答案

名师金手指大试卷系列答案

标准课堂测试卷系列答案

智慧翔夺冠金卷系列答案

名校导练系列答案

目标实施手册测试卷系列答案

智慧通自主练习系列答案

第一微卷系列答案

相关题目

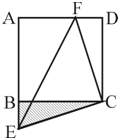如图所示，设F为正方形ABCD边AD上一点，CE⊥CF交AB的延长线于E，若正方形ABCD的面积为64，△CEF的面积为50，则△CBE的面积为

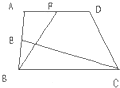如图所示，在梯形ABCD中，E是AB的中点，F是AD的中点．已知△BCE的面积为6平方厘米，△ABF的面积为4平方厘米，则梯形ABCD的面积为

平方厘米．

如图，若△ABC的面积是24，D、E、F分别是BC、AD、AB的中点，则△BEF的面积是

如图，ABCD是梯形，E是AD的中点，直线CE把梯形分成甲乙两部分，它们的面积之比是
13：9那么AB：CD=

如图，在△ABC中，E、D、F分别为AD、BC、AB的中点，BD=DE=EC，BF=FA，△EDF的面积是1，那么△ABC的面积是多少？