题目内容
 如图,ABCD是梯形,E是AD的中点,直线CE把梯形分成甲乙两部分,它们的面积之比是
如图,ABCD是梯形,E是AD的中点,直线CE把梯形分成甲乙两部分,它们的面积之比是13:9那么AB:CD=
2:9
2:9
.分析:连接AC,因为E是中点,所以三角形AEC和三角形DEC的面积相等,甲乙两部分,它们的面积之比是13:9,把乙看做是9,则三角形AEC的面积就是9,则三角形ABC的面积就是13-9=4,由此可得出三角形ABC与三角形ADC的面积之比是4:(9+9)=4:18=2:9,因为三角形ABC与三角形ADC的高相等,所以面积与底成正比例,所以AB:CD=2:9.
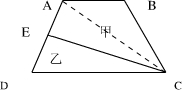

解答:解:连接AC,根据题干可得:把乙看做是9,则三角形AEC的面积就是9,
因为E是中点,所以三角形AEC和三角形DEC的面积相等,
则三角形ABC的面积就是13-9=4,
所以三角形ABC与三角形ADC的面积之比是4:(9+9)=4:18=2:9,
所以AB:CD=2:9.
故答案为:2:9.
因为E是中点,所以三角形AEC和三角形DEC的面积相等,
则三角形ABC的面积就是13-9=4,
所以三角形ABC与三角形ADC的面积之比是4:(9+9)=4:18=2:9,
所以AB:CD=2:9.
故答案为:2:9.
点评:此题考查高一定时,三角形的面积与底成正比的关系的灵活应用,关键利用辅助线是把AB与CD放在同高的两个三角形中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
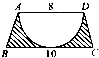
 (2009?崇文区)如图,ABCD是直角梯形,已知OE垂直于DC,AD=10厘米,三角形BOC面积为15平方厘米,那么三角形ADO的面积是
(2009?崇文区)如图,ABCD是直角梯形,已知OE垂直于DC,AD=10厘米,三角形BOC面积为15平方厘米,那么三角形ADO的面积是 如图,ABCD是梯形,AD平行于BC,BC=2AD,M是BC的中点,N是BM的中点,P是AD的中点,则△NCD的面积是△ANP的面积的多少倍?
如图,ABCD是梯形,AD平行于BC,BC=2AD,M是BC的中点,N是BM的中点,P是AD的中点,则△NCD的面积是△ANP的面积的多少倍?