题目内容
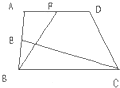 如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为
如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为20
20
平方厘米.分析:如图,连结BD,由于E是AB的中点,△BCE的高是梯形ABCD高的一半,也是△DBC高的一半,因此,△BCE的面积等于△DBC面积的一半;由于F是AD的中点,△ABF与梯形ABCD,△ABD等高,面积是△ABD面积的一半,因为△ABD的面积+△DBC的面积=梯形ABCD的面积,所以△BCE的面积+△EBC的面积=梯形ABCD面积的一半,据此解答.
解答:解:如图,
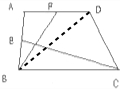
连结BD,由题意可知,S△BCE=
S△DBC,S△ABF=
S△ABD,
S△BCE+S△ABF=
(S△DBC+S△ABD),
由于S△DBC+S△ABD=S梯形ABCD,
所以S梯形ABCD=2(S△BCE+S△ABF)
=2(6+4)
=2×10
=20(平方厘米);
故答案为:20

连结BD,由题意可知,S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
S△BCE+S△ABF=
| 1 |
| 2 |
由于S△DBC+S△ABD=S梯形ABCD,
所以S梯形ABCD=2(S△BCE+S△ABF)
=2(6+4)
=2×10
=20(平方厘米);
故答案为:20
点评:本题利用梯形的面积公式不能求出梯形的面积,巧妙是作一辅助线,把梯形分成两个三角形,由题意可知,这两个三角形又分别是两个已知三角形面积的2倍,由此得解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

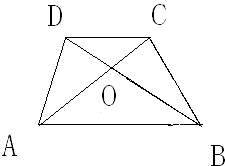 如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=6,CD=4,梯形ABCD的面积为5,求三角形OBC的面积.
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=6,CD=4,梯形ABCD的面积为5,求三角形OBC的面积.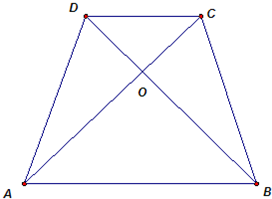 如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.
如图所示,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O.已知AB=5,CD=3,且梯形ABCD的面积为4,求三角形OAB的面积.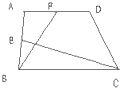 如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为________平方厘米.
如图所示,在梯形ABCD中,E是AB的中点,F是AD的中点.已知△BCE的面积为6平方厘米,△ABF的面积为4平方厘米,则梯形ABCD的面积为________平方厘米.