题目内容
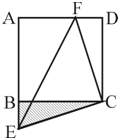 如图所示,设F为正方形ABCD边AD上一点,CE⊥CF交AB的延长线于E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为
如图所示,设F为正方形ABCD边AD上一点,CE⊥CF交AB的延长线于E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为24
24
.分析:根据△CEF的面积=梯形AECD的面积-△CDF的面积-△AEF的面积计算可求得答案.
解答:解:由题意可知△CBE的面积=△CDF的面积,设BE=DF=x,
则△CEF的面积=梯形AECD的面积-△CDF的面积-△AEF的面积,
所以
-
-
=50,
解得x=6,
所以△CBE的面积=6×8÷2=24.
故答案为:24.
则△CEF的面积=梯形AECD的面积-△CDF的面积-△AEF的面积,
所以
| 8×(8+x+8) |
| 2 |
| 8x |
| 2 |
| (8+x)(8-x) |
| 2 |
解得x=6,
所以△CBE的面积=6×8÷2=24.
故答案为:24.
点评:解决本题的关键是得到△CEF的面积表示方法.

练习册系列答案
相关题目
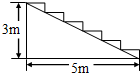 某宾馆重新装修后,准备在大厅的主楼梯上铺设某种红地毯.已知这种地毯的售价为62.5元/m2,主楼梯道宽2m,其侧面图如图所示.请你为宾馆老板预算一下,购买地毯至少需要多少钱?
某宾馆重新装修后,准备在大厅的主楼梯上铺设某种红地毯.已知这种地毯的售价为62.5元/m2,主楼梯道宽2m,其侧面图如图所示.请你为宾馆老板预算一下,购买地毯至少需要多少钱?
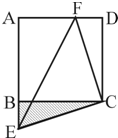 如图所示,设F为正方形ABCD边AD上一点,CE⊥CF交AB的延长线于E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为________.
如图所示,设F为正方形ABCD边AD上一点,CE⊥CF交AB的延长线于E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为________.