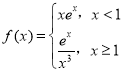【题目】随着人们生活水平的不断提高,肥胖人数不断增多.世界卫生组织(WHO)常用身体质量指数(BMI)来衡量人体胖瘦成度以及是否健康,其计算公式是![]() .成人的BMI数值标准为:BMI
.成人的BMI数值标准为:BMI![]() 偏瘦;
偏瘦;![]() BMI
BMI![]() 为正常;
为正常;![]() BMI
BMI![]() 为偏胖;BMI
为偏胖;BMI![]() 为肥胖.某研究机构为了解某快递公司员工的身体质量指数,研究人员从公司员工体检数据中,抽取了8名员工(编号1-8)的身高
为肥胖.某研究机构为了解某快递公司员工的身体质量指数,研究人员从公司员工体检数据中,抽取了8名员工(编号1-8)的身高![]() (cm)和体重
(cm)和体重![]() (kg)数据,并计算得到他们的BMI(精确到0.1)如下表:
(kg)数据,并计算得到他们的BMI(精确到0.1)如下表:
编 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 163 | 164 | 165 | 168 | 170 | 172 | 176 | 182 |
体重(kg) | 54 | 60 | 77 | 72 | 68 | ● | 72 | 55 |
BMI(近似值) | 20.3 | 22.3 | 28.3 | 25.5 | 23.5 | 23.7 | 23.2 | 16.6 |
(1)现从这8名员工中选取3人进行复检,记抽取到BMI值为“正常”员工的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(2)研究机构分析发现公司员工的身高![]() (cm)和体重
(cm)和体重![]() (kg)之间有较强的线性相关关系,在编号为6的体检数据丢失之前调查员甲已进行相关的数据分析,并计算得出该组数据的线性回归方程为
(kg)之间有较强的线性相关关系,在编号为6的体检数据丢失之前调查员甲已进行相关的数据分析,并计算得出该组数据的线性回归方程为![]() ,且根据回归方程预估一名身高为180cm的员工体重为71kg,计算得到的其它数据如下:
,且根据回归方程预估一名身高为180cm的员工体重为71kg,计算得到的其它数据如下:![]() ,
,![]() .
.
①求![]() 的值及表格中8名员工体重的平均值
的值及表格中8名员工体重的平均值![]() .
.
②在数据处理时,调查员乙发现编号为8的员工体重数据有误,应为63kg,身高数据无误,请你根据调查员乙更正的数据重新计算线性回归方程,并据此预估一名身高为180cm的员工的体重.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: 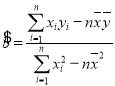 ,
,![]() .
.