【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的质量(单位:克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/克 | 频数 |
(490,495] | 6 |
(495,500] | 8 |
(500,505] | 14 |
(505,510] | 8 |
(510,515] | 4 |

甲流水线样本频数分布表:
甲流水线 | 乙流水线 | 总计 | |
合格品 |
|
| |
不合格品 |
|
| |
总计 |
|
(1)根据上表数据作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从乙流水线任取![]() 件产品,该产品恰好是合格品的概率;
件产品,该产品恰好是合格品的概率;
(3)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为产品的包装质量与两条自动包装流水线的选择有关?
的前提下认为产品的包装质量与两条自动包装流水线的选择有关?
附表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式:  )
)
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
储蓄存款 | 6 | 7 | 8 | 9 | 10 |
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)用所求回归方程预测该地区2015年![]() 的人民币储蓄存款.
的人民币储蓄存款.
附:回归方程![]() 中,
中, 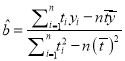 ,
,
【题目】随着国民生活水平的提高,利用长假旅游的人越来越多,其公司统计了2012到2016年五年间本公司职工每年春节期间外出旅游的家庭数,具体统计数据如表所示:
年份x | 2012 | 2013 | 2014 | 2015 | 2016 |
家庭数y | 6 | 10 | 16 | 22 | 26 |
(1)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程y=bx+a,判断它们之间是否是正相关还是负相关;
(2)根据所求的直线方程估计该公司2019年春节期间外出的旅游的家庭数.
