【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
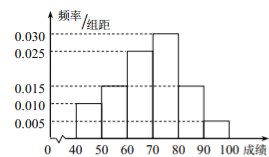
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(1)填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取![]() 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
附表及公式:
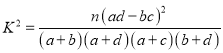 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】宿州市某登山爱好者为了解山高y(百米)与气温x(℃)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表,由表中数据,得到线性回归方程为y=﹣2x+a,由此估计山高为72(百米)处的气温为( )
气温x(℃) | 18 | 13 | 10 | ﹣1 |
山高y(百米) | 24 | 34 | 38 | 64 |
A.﹣10
B.﹣8
C.﹣6
D.﹣4