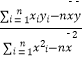题目内容
【题目】已知等比数列{an}是单调递增的数列,a2+a3+a4=28,且a3+2是a2 , a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=anlog2an , 数列{bn}的前n项和为Sn , 求Sn .
【答案】
(1)解:设等比数列{an}的首项a1,公比为q,q>0,
依题意可得:2(a3+2)=a2+a4,代入a2+a3+a4=28,
解得:a3=8,a2+a4=20,
∴ ![]() ,
,
解得: ![]() 或
或  ,
,
∵数列{an}是单调递增的数列,
∴a1=2,q=2,
∴数列{an}的通项公式为an=2n
(2)解:∵bn=anlog2an=n2n,
∴Sn=1×2+2×22+3×23+…+n2n,①
2Sn=1×22+2×23+3×24+…+n2n+1,②
①﹣②,得﹣Sn=2+22+23+…+2n﹣n2n+1,
= ![]() ﹣n2n+1,
﹣n2n+1,
=2n+1﹣n2n+1﹣2,
=(1﹣n)2n+1﹣2,
∴Sn=(n﹣1)2n+1+2
【解析】(1)由2(a3+2)=a2+a4 , 代入a2+a3+a4=28,求得a3=8,a2+a4=20,根据等比数列通项公式,即可求a1=2,q=2,求得数列{an}的通项公式;(2)由bn=anlog2an=n2n , 采用“错位相减法”即可求得数列{bn}的前n项和为Sn .
【考点精析】利用数列的前n项和对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系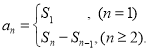 .
.

【题目】宿州市某登山爱好者为了解山高y(百米)与气温x(℃)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表,由表中数据,得到线性回归方程为y=﹣2x+a,由此估计山高为72(百米)处的气温为( )
气温x(℃) | 18 | 13 | 10 | ﹣1 |
山高y(百米) | 24 | 34 | 38 | 64 |
A.﹣10
B.﹣8
C.﹣6
D.﹣4