Question

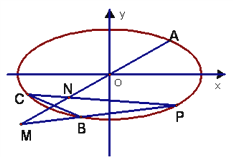
【题目】如图，在平面直角坐标系中，已知A、B、C是椭圆上不同的三点， ，C在第三象限，线段BC的中点在直线OA上。

（1）求椭圆的标准方程；

（2）求点C的坐标；

（3）设动点P在椭圆上（异于点A、B、C）且直线PB， PC分别交直线OA于M、N两点，证明为定值并求出该定值.

Answer 1

【答案】（1）（2）点的坐标为．（3）为定值，定值为．

【解析】试题分析：（1）将点A，B的坐标代入方程即可求得，（2）设点，得BC的中点坐标，带去直线OA联立椭圆方程即可求得m,n,从而得C的坐标，（3）分别设出P,N,M三点坐标，根据P,B,M三点共线和P,C,N三点共线得到M，N,P的关系，将P点坐标代入椭圆方程即可得各系数之间的关系，于是化简得定制

试题解析：

解：（1）由已知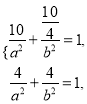，得 解得

所以椭圆的标准方程为．

（2）设点 ，则中点为．

由已知，求得直线的方程为，从而．①

又∵点在椭圆上，∴．②

由①②，解得（舍），，从而． 所以点的坐标为．

（3）设， ， ．

∵三点共线，∴，整理，得．

∵三点共线，∴，整理，得．

∵点在椭圆上，∴， ．

从而．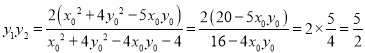

所以．∴为定值，定值为．