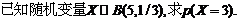|
课题:独立重复试验与二项分布 |
||||
|
1.在相同条件下重复做的n次试验称为n次独立重复试验. 2.若一次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生K次的概率为. 
3. |
学生演板例题解答过程 |
(三).信息交流 揭示规律
问题2的解决:(学生拿自己的草稿在投影下讲)
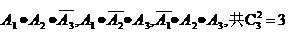 分别记在第1,2,3次射击中,该同学击破气球为事件A1,A2,A3,那么射击3次,击破2个共有下面三种情况:,
种,每一种情况的概率为
分别记在第1,2,3次射击中,该同学击破气球为事件A1,A2,A3,那么射击3次,击破2个共有下面三种情况:,
种,每一种情况的概率为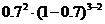 ,因为三种情况彼此互斥,故3次射击击破2个的概率
,因为三种情况彼此互斥,故3次射击击破2个的概率
|
x |
0 |
1 |
2 |
3 |
|
p |
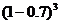 |
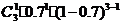 |
 |
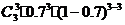 |
X的分布列:
而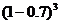 +
+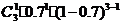 +
+ +
+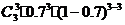
=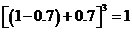
设计意图: 上述解答是一个前面所学知识的应用过程 . 学生看到最后的结果,有一种``拨开云雾看清天”的感觉,这不就是二项式定理吗?学生热情高涨,课堂达到高潮,把对知识的学习掌握变成了对知识的探索 、发现、总结、创新的过程.
通过解决问题2,学生在老师引导下,由特殊到一般,由具体到抽象,由n次独立重复试验发生k次的概率,主动建构二项分布这一重要的离散型随机变量的分布列.攻破本节课的难点。
2.二项分布模型的构建(这一过程师生共同完成):
若一次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生K次的概率为. 

以事件A发生的次数X为随机变量,则X的分布列为:
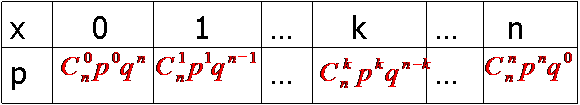

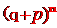
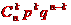
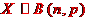 其中的
是二项式
展开式中的通项,故称X服从二项分布。记为
,其中 n,p 为参数, n表示重复的次数,p指一次试验中事件A发生的概率。
其中的
是二项式
展开式中的通项,故称X服从二项分布。记为
,其中 n,p 为参数, n表示重复的次数,p指一次试验中事件A发生的概率。
深化认识:
二项分布是一种概率模型,有着十分广泛的应用。用以解决独立重复试验中的概率问题.比如下列问题中的随机变量ξ都可以看作是服从二项分布的:
n n次独立射击,每次命中率相同,ξ为命中次数。
n 一枚硬币掷n次,ξ为正面出现的次数。
n 掷n个相同的骰子,ξ为一点出现的次数。
n n个新生婴儿,ξ为男婴的个数。
n 女性患色盲的概率为0.25%,ξ为任取n个女人中患色盲的人数。(这一过程约8分钟)
设计意图:从实际中来,到实际中去,抽象出的二项分布有何用途?什么时候用?这是学生想知道的。也是我们学习数学的目的所在。
怎么用呢?导入下一个环节。
 (2008·镇江模拟)右图中秦代砖文为“海内皆臣,岁登成熟,道毋饥人”。其中“海内皆臣”
(2008·镇江模拟)右图中秦代砖文为“海内皆臣,岁登成熟,道毋饥人”。其中“海内皆臣”


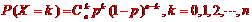
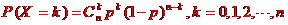 3.事件A恰好发生K次的概率为:
3.事件A恰好发生K次的概率为: