20、解析:(Ⅰ)当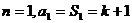 ,
,
 (
( )
)
经验, (
( )式成立,
)式成立,

(Ⅱ) 成等比数列,
成等比数列,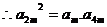 ,
,
即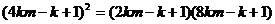 ,整理得:
,整理得: ,
,
对任意的 成立,
成立,

|

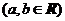 .
.
(I)若函数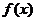 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,求
,求 的值;
的值;
(II)若函数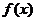 在区间
在区间 上不单调,求
上不单调,求 的取值范围.
的取值范围.
解析:(Ⅰ)由题意得
又 ,解得
,解得 ,
,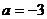 或
或
(Ⅱ)函数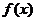 在区间
在区间 不单调,等价于
不单调,等价于
导函数 在
在 既能取到大于0的实数,又能取到小于0的实数
既能取到大于0的实数,又能取到小于0的实数
即函数 在
在 上存在零点,根据零点存在定理,有
上存在零点,根据零点存在定理,有
 , 即:
, 即:
整理得: ,解得
,解得

|
 :
: 上一点
上一点 到其焦点的距离为
到其焦点的距离为 .
.
(I)求 与
与 的值;
的值;
(II)设抛物线 上一点
上一点 的横坐标为
的横坐标为 ,过
,过 的直线交
的直线交 于另一点
于另一点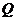 ,交
,交 轴于
轴于
点 ,过点
,过点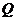 作
作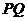 的垂线交
的垂线交 于另一点
于另一点 .若
.若 是
是 的切线,求
的切线,求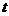 的最小值.
的最小值.
19.(Ⅰ)证明:连接 , 在
, 在 中,
中, 分别是
分别是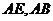 的中点,所以
的中点,所以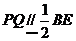 , 又
, 又 ,所以
,所以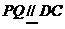 ,又
,又 平面ACD ,DC
平面ACD ,DC 平面ACD, 所以
平面ACD, 所以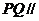 平面ACD
平面ACD
(Ⅱ)在 中,
中, ,所以
,所以
而DC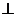 平面ABC,
平面ABC, ,所以
,所以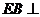 平面ABC
平面ABC
而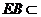 平面ABE, 所以平面ABE
平面ABE, 所以平面ABE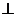 平面ABC, 所以
平面ABC, 所以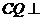 平面ABE
平面ABE
由(Ⅰ)知四边形DCQP是平行四边形,所以
所以 平面ABE, 所以直线AD在平面ABE内的射影是AP,
平面ABE, 所以直线AD在平面ABE内的射影是AP,
所以直线AD与平面ABE所成角是
在 中,
中, ,
,
所以
|
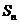 为数列
为数列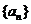 的前
的前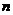 项和,
项和,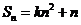 ,
, ,其中
,其中 是常数.
是常数.
(I) 求 及
及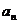 ;
;
(II)若对于任意的 ,
,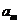 ,
, ,
, 成等比数列,求
成等比数列,求 的值.
的值.
|
 中,角
中,角 所对的边分别为
所对的边分别为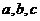 ,且满足
,且满足 ,
,
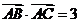 .
(I)求
.
(I)求 的面积;
(II)若
的面积;
(II)若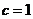 ,求
,求 的值.
的值.
18.解析:(Ⅰ)
又 ,
,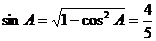 ,而
,而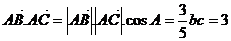 ,所以
,所以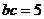 ,所以
,所以 的面积为:
的面积为: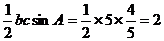
(Ⅱ)由(Ⅰ)知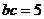 ,而
,而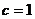 ,所以
,所以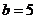
所以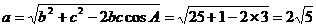

|
 平面
平面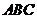 ,
, ,
, ,
, ,
, 分别为
分别为 的中点.(I)证明:
的中点.(I)证明: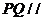 平面
平面 ;(II)求
;(II)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 K-介子衰变方程为:K-→?π-?+π0,其中K-介子和π-介子带负的基元电荷,π0介子不带电.如图所示,一个K-介子沿垂直于磁场的方向射入匀强磁场中,其轨迹为圆弧AP,衰变后产生的π-介子的轨迹为圆弧PB,两轨迹在P点相切,它们的半径R1与R2之比为2∶1,π0介子的轨迹未画出.由此可知π-的动量大小与π0的动量大小之比为 ( A )
K-介子衰变方程为:K-→?π-?+π0,其中K-介子和π-介子带负的基元电荷,π0介子不带电.如图所示,一个K-介子沿垂直于磁场的方向射入匀强磁场中,其轨迹为圆弧AP,衰变后产生的π-介子的轨迹为圆弧PB,两轨迹在P点相切,它们的半径R1与R2之比为2∶1,π0介子的轨迹未画出.由此可知π-的动量大小与π0的动量大小之比为 ( A )  训练题如图所示,一个带负电的滑环套在水平且足够长的粗糙的绝缘杆上,整个装置处于方向如图所示的匀强磁场B中.现给滑环施以一个水平向右的瞬时冲量,使其由静止开始运动,则滑环在杆上的运动情况可能是 ( ABC )
训练题如图所示,一个带负电的滑环套在水平且足够长的粗糙的绝缘杆上,整个装置处于方向如图所示的匀强磁场B中.现给滑环施以一个水平向右的瞬时冲量,使其由静止开始运动,则滑环在杆上的运动情况可能是 ( ABC ) 匀强磁场中,穿透磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是,穿透磁场的时间是 .
匀强磁场中,穿透磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是,穿透磁场的时间是 . (1)若B0 = B1为已知量,试求离子在磁场中运动时的轨道半径R及周期的表达式.
(1)若B0 = B1为已知量,试求离子在磁场中运动时的轨道半径R及周期的表达式.

 可能详细地论述此磁场的分布情况,不考虑重力的影响。
可能详细地论述此磁场的分布情况,不考虑重力的影响。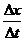 =
=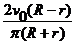 (2)论述略,
(2)论述略,
 ,根据抛物线定义
,根据抛物线定义 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即 ,解得
,解得
 抛物线方程为:
抛物线方程为: ,将
,将
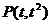 的直线
的直线 ,当
,当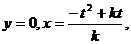 则
则 。
。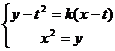 ,整理得:
,整理得:
 ,解得
,解得 或
或
 ,而
,而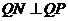 ,
,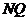 斜率为
斜率为
 ,联立方程
,联立方程
 ,即:
,即: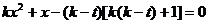
 ,解得:
,解得: ,或
,或 ,
,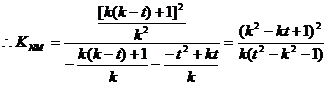

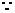 MN是抛物线的切线,
MN是抛物线的切线, , 整理得
, 整理得
 ,解得
,解得 (舍去),或
(舍去),或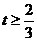 ,
,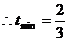
 [命题意图]此题是一个排列组合问题,既考查了分析问题,解决问题的能力,更侧重于考查学生便举问题解决实际困难的能力和水平
[命题意图]此题是一个排列组合问题,既考查了分析问题,解决问题的能力,更侧重于考查学生便举问题解决实际困难的能力和水平 ,而基本事件有20种,因此
,而基本事件有20种,因此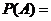
 张卡片,每张卡片上分别标有两个连续的自然数
张卡片,每张卡片上分别标有两个连续的自然数 ,其中
,其中 .
. 的卡片,则卡片上两个数的各位数字之和为
的卡片,则卡片上两个数的各位数字之和为 )不小于
)不小于 ”为
”为 ,
, [命题意图]此题是一个数列与类比推理结合的问题,既考查了数列中等差数列和等比数列的知识,也考查了通过已知条件进行类比推理的方法和能力
[命题意图]此题是一个数列与类比推理结合的问题,既考查了数列中等差数列和等比数列的知识,也考查了通过已知条件进行类比推理的方法和能力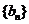 的前
的前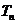 ,则
,则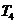 ,
,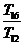 成等比数列.
成等比数列.