所以
由事件的独立性的

解答2(Ⅰ)设事件A表示“一个月内被投诉2次”设事件B表示“一个月内被投诉的次数不超过1次”
所以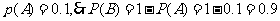
(Ⅱ)同解答1(Ⅱ)
29、(2009湖南卷理)(本小题满分12分) 
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的. 、
、 、
、 ,现在3名工人独立地从中任选一个项目参与建设。
,现在3名工人独立地从中任选一个项目参与建设。


(I)求他们选择的项目所属类别互不相同的概率;
(II)记 为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求
为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求 的分布列及数学期望。
的分布列及数学期望。
解:记第1名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件
 ,
, ,
, ,i=1,2,3.由题意知
,i=1,2,3.由题意知
 相互独立,
相互独立,
 相互独立,
相互独立,
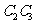 相互独立,
相互独立, ,
, ,
, (i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P(
(i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P( )=,P(
)=,P( )=
)= ,P(
,P( )=
)=
(1)他们选择的项目所属类别互不相同的概率
P=3!P(

 )=6P(
)=6P( )P(
)P( )P(
)P( )=6
)=6




 =
=
(2) 解法1 设3名工人中选择的项目属于民生工程的人数为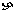 ,由己已知,
,由己已知,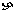 -B(3,
-B(3, ),且
),且 =3
=3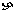 。
。
所以P( =0)=P(
=0)=P(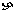 =3)=
=3)=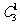
 =
=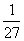 ,
, 
P( =1)=P(
=1)=P(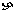 =2)=
=2)= 

 =
=



P( =2)=P(
=2)=P(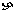 =1)=
=1)=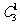

 =
=
P( =3)=P(
=3)=P(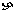 =0)=
=0)= 
 =
=
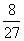
故 的分布是
的分布是
 |
0 |
1 |
2 |
3 |
|
P |
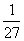 |
 |
 |
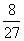 |
 的数学期望E
的数学期望E =0
=0
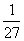 +1
+1
 +2
+2
 +3
+3
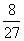 =2
=2
解法2 第i名工人选择的项目属于基础工程或产业工程分别为事件 ,
,
i=1,2,3 ,由此已知, ·D,
·D, 相互独立,且
相互独立,且
P( )-(
)-( ,
, )= P(
)= P( )+P(
)+P( )=
)= +
+ =
=

所以 --
-- ,既
,既 ,
,


故 的分布列是
的分布列是
 |
 |
1 |
2 |
3 |
 |
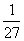 |
 |
 |
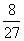 |
22、(2009安徽卷理)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是 .同样也假定D受A、B和C感染的概率都是
.同样也假定D受A、B和C感染的概率都是 .在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
本小题主要考查古典概型及其概率计算,考查取有限个值的离散型随机变量及其分布列和均值的概念,通过设置密切贴近现实生活的情境,考查概率思想的应用意识和创新意识。体现数学的科学价值。本小题满分12分。
解 随机变量X的分布列是
|
X |
1 |
2 |
3 |
|
P |
 |
 |
 |
X的均值为
附:X的分布列的一种求法
共有如下6种不同的可能情形,每种情形发生的概率都是 :
:
|
① |
② |
③ |
④ |
⑤ |
⑥ |
|
A-B-C-D |
A-B-C └D |
A-B-C └D |
A-B-D └C |
A-C-D └B |
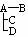 |
在情形①和②之下,A直接感染了一个人;在情形③、④、⑤之下,A直接感染了两个人;在情形⑥之下,A直接感染了三个人。
21、(2009山东卷理)(本小题满分12分)
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3
分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第
三次,某同学在A处的命中率q 为0.25,在B处的命中率为q
为0.25,在B处的命中率为q ,该同学选择先在A
,该同学选择先在A
处投一球,以后都在B处投,用 表示该同学投篮训练结束后所得的总分,其分布列
表示该同学投篮训练结束后所得的总分,其分布列
为
 |
0
|
2
|
3 |
4 |
5 |
  p p
|
0.03
|
P1
|
P2 |
P3
|
P4
|
(1)求q 的值;
的值; 

(2)求随机变量 的数学期望E
的数学期望E ;
;
(3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
解 (1)设该同学在A处投中为事件A,在B处投中为事件B,则事件A,B相互独立,且P(A)=0.25, ,
P(B)= q
,
P(B)= q ,
, .
.
根据分布列知:  =0时
=0时 =0.03,所以
=0.03,所以
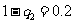 ,q
,q =0.8.
=0.8.
(2)当 =2时, P1=
=2时, P1=


 =0.75 q
=0.75 q (
(
 )×2=1.5 q
)×2=1.5 q (
(
 )=0.24
)=0.24
当 =3时, P2 =
=3时, P2 = =0.01,
=0.01,
当 =4时, P3=
=4时, P3= =0.48,
=0.48,
当 =5时, P4=
=5时, P4=
 =0.24
=0.24
所以随机变量 的分布列为
的分布列为
 |
0
|
2
|
3 |
4 |
5 |
|
p
|
0.03
|
0.24
|
0.01 |
0.48
|
0.24
|
随机变量 的数学期望
的数学期望
(3)该同学选择都在B处投篮得分超过3分的概率为

 ;
;
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72.
由此看来该同学选择都在B处投篮得分超过3分的概率大.
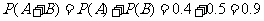
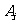 表示“第
表示“第 个月被投诉的次数为0”事件
个月被投诉的次数为0”事件 表示“第
表示“第 表示“第
表示“第

 局甲获胜”为事件
局甲获胜”为事件 ,“第
,“第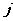 局甲获胜”为事件
局甲获胜”为事件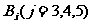 。
。 ,由于各局比赛结果相互独立,故
,由于各局比赛结果相互独立,故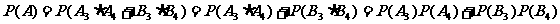
 。
。 ,由于各局比赛结果相互独立,故
,由于各局比赛结果相互独立,故

 i=1,2,3.由题意知
i=1,2,3.由题意知 相互独立,
相互独立,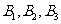 相互独立,
相互独立,
 (i,j,k=1,2,3,且i,j,k互不相同)相互独立,
(i,j,k=1,2,3,且i,j,k互不相同)相互独立,

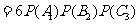

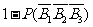



 ,
,

 ……
…… ,求
,求 、6、
、6、 11取,则有
11取,则有
 的分布列为
的分布列为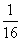



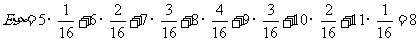 .
. .
. 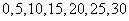
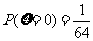






 .
.  .
. ”等价于事件“该学生在路上遇到
”等价于事件“该学生在路上遇到 次红灯”(
次红灯”( 0,1,2,3,4),
0,1,2,3,4), ,
,

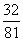

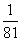
 .
.