摘要：例4.在直角梯形ABCD中.∠A=∠D=90°.AB＜CD.SD⊥平面ABCD.AB=AD=a.S D=.在线段SA上取一点E使EC=AC.截面CDE与SB交于点F.(1)求证:四边形EFCD为直角梯形,(2)求二面角B-EF-C的平面角的正切值,(3)设SB的中点为M.当的值是多少时.能使△DMC为直角三角形?请给出证明.解:(1)∵ CD∥AB.AB平面SAB ∴CD∥平面SAB面EFCD∩面SAB=EF.∴CD∥EF ∵又面 ∴ 平面SAD.∴又 为直角梯形 (2)平面∥平面SAD 即为二面角D―EF―C的平面角 中而且为等腰三角形. (3)当时.为直角三角形 . ,平面平面.在中.为SB中点..平面平面 为直角三角形.
网址：http://m.1010jiajiao.com/timu_id_78007[举报]
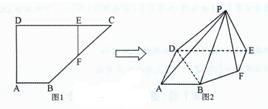如图1，在直角梯形ABCD中，AB∥CD，∠A=90°，AB=2，CD=6，AD=3，E为CD上一点，且DE=4，过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF，使∠PED=60°，如图2．（Ⅰ）求证：PE⊥平面ADP；
（Ⅱ）求异面直线BD与PF所成角的余弦值；
（Ⅲ）在线段PF上是否存在一点M，使DM与平在ADP所成的角为30°？若存在，确定点M的位置；若不存在，请说明理由． 查看习题详情和答案>>
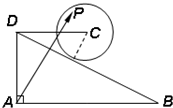（2012•洛阳模拟）如图，在直角梯形ABCD中，AD⊥AB，AB∥DC，AD=DC=1，AB=2，动点P在以点C为圆心，且与直线BD相切的圆上或圆内移动，设| AP |
| AD |
| AB |
查看习题详情和答案>>
如图，在直角梯形ABCD中，已知BC∥AD，AB⊥AD，AB=4，BC=2，AD=4，若P为CD的中点，则
如图，在直角梯形ABCD中，AD⊥AB，BC⊥AB，AD=3，AB=4，BC=