题目内容
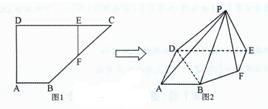 如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.
如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.(Ⅰ)求证:PE⊥平面ADP;
(Ⅱ)求异面直线BD与PF所成角的余弦值;
(Ⅲ)在线段PF上是否存在一点M,使DM与平在ADP所成的角为30°?若存在,确定点M的位置;若不存在,请说明理由.
分析:(Ⅰ)由题设条件及图形知,本题可采用两种方法求解,
法一,证明AD⊥PE,PE⊥PD,再利用线面垂直的判定定理证明即可;
法二,用向量法,建立如图的坐标系,根据题设条件写出各点的坐标,易得直线PE的方向向量与面内两直线AD,PD的方向向量,用数量积证明即可;
(Ⅱ)本题用向量法比较方便,借助(I)中的坐标系,易得两异面直线的方向向量,用数量积求两异面直线的夹角的余弦值或其补角的余弦值;
(Ⅲ)先假定存在,设出点M的坐标,由线面垂直的条件寻求满足题意的条件,根据DM与平在ADP所成的角为30°,建立方程求参数,为了解答本题,需要求出平面的法向量与直线DM的方向向量.然后利用相关规则求夹角的余弦,令其值等于sin30°,建立方程求参数,若能求出符合条件的参数,则说明存在,否则,说明不存在.
法一,证明AD⊥PE,PE⊥PD,再利用线面垂直的判定定理证明即可;
法二,用向量法,建立如图的坐标系,根据题设条件写出各点的坐标,易得直线PE的方向向量与面内两直线AD,PD的方向向量,用数量积证明即可;
(Ⅱ)本题用向量法比较方便,借助(I)中的坐标系,易得两异面直线的方向向量,用数量积求两异面直线的夹角的余弦值或其补角的余弦值;
(Ⅲ)先假定存在,设出点M的坐标,由线面垂直的条件寻求满足题意的条件,根据DM与平在ADP所成的角为30°,建立方程求参数,为了解答本题,需要求出平面的法向量与直线DM的方向向量.然后利用相关规则求夹角的余弦,令其值等于sin30°,建立方程求参数,若能求出符合条件的参数,则说明存在,否则,说明不存在.
解答: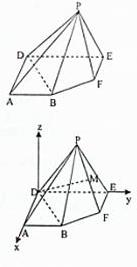 解:(Ⅰ)解法一:∵DE=4,PE=2,∠PED=60°,由弦定理得PD=2
解:(Ⅰ)解法一:∵DE=4,PE=2,∠PED=60°,由弦定理得PD=2
,
∵PD2+PE2=16=DE2,∴PE⊥PD.∵EF⊥PE,EF⊥DE∴,EF⊥平面PDE,又∵EF∥AD,∴AD⊥平面PDE,∴AD⊥PE,又∵直线AD,PD在平面APD内,且相交于D,∴PE⊥平面APD.
解法二:EF⊥PE,EF⊥DE∴,EF⊥平面PDE∴平面DEF⊥平面PDE
以DA所在的直线为 x轴,以DE所在的直线为y轴,在平面DPE内过D作DE的垂线,以垂线所在直线为z轴,建立空间直角坐标系,如图
则D(0,0,0),A(3,0,0),P(0,3,
),E(0,4,0)
∴
=(3,0,0),
=(0,3,
),
=(0,-1,
).∵
•
=0,
•
=0,∴
⊥
,
⊥
∴DA⊥EP,DP⊥EP,∵DA,DP是平面ADP内的相交直线,∴PE⊥平面APD.
(Ⅱ)由(Ⅰ)知AD⊥平面PDE,∴平面ADE⊥平面PDE
以DA所在的直线为 x轴,以DE所在的直线为y轴,在平面DPE内过D作DE的垂线,以垂线所在直线为z轴,建立空间直角坐标系,如图
则D(0,0,0),A(3,0,0),P(0,3,
),E(0,4,0),F(
,4,0),B(3,2,0),∴
=(3,2,0),
=(
,1,-
)
∴cos<
,
> =
=
设BD与PF所成的角为θ,则θ=<
,
>,∴cosθ=
(Ⅲ)由(Ⅱ)知
=(0,-1,
).
=(
,1,-
)
∵PE⊥平面ADP,∴平面ADP的法向量为
=
=(0,-1,
).
设M是线段PF上一点,则存在0≤λ≤1,
使
=λ
∴
=
+
═(0,3,
)+λ(
,1,-
)=(
λ,λ+3,-
λ+3)
.cos<
,
>=
=
,如果直线DM与平面ADC所成的角为30°,
那么|cos<
,
>|=sin30°,即
=±
解得λ2=
∵此方程在[0,1]内无解,
∴在线段PF上不存在一点M,使DM与平在ADP所成的角为30°.
 解:(Ⅰ)解法一:∵DE=4,PE=2,∠PED=60°,由弦定理得PD=2
解:(Ⅰ)解法一:∵DE=4,PE=2,∠PED=60°,由弦定理得PD=2| 3 |
∵PD2+PE2=16=DE2,∴PE⊥PD.∵EF⊥PE,EF⊥DE∴,EF⊥平面PDE,又∵EF∥AD,∴AD⊥平面PDE,∴AD⊥PE,又∵直线AD,PD在平面APD内,且相交于D,∴PE⊥平面APD.
解法二:EF⊥PE,EF⊥DE∴,EF⊥平面PDE∴平面DEF⊥平面PDE
以DA所在的直线为 x轴,以DE所在的直线为y轴,在平面DPE内过D作DE的垂线,以垂线所在直线为z轴,建立空间直角坐标系,如图
则D(0,0,0),A(3,0,0),P(0,3,
| 3 |
∴
| DA |
| DP |
| 3 |
| EP |
| 3 |
| DA |
| EP |
| DP |
| EP |
| DA |
| EP |
| DP |
| EP |
(Ⅱ)由(Ⅰ)知AD⊥平面PDE,∴平面ADE⊥平面PDE
以DA所在的直线为 x轴,以DE所在的直线为y轴,在平面DPE内过D作DE的垂线,以垂线所在直线为z轴,建立空间直角坐标系,如图
则D(0,0,0),A(3,0,0),P(0,3,
| 3 |
| 3 |
| 2 |
| DB |
| PF |
| 3 |
| 2 |
| 3 |
∴cos<
| DB |
| PF |
| ||||
|
|
| ||
| 5 |
设BD与PF所成的角为θ,则θ=<
| DB |
| PF |
| ||
| 5 |
(Ⅲ)由(Ⅱ)知
| EP |
| 3 |
| PF |
| 3 |
| 2 |
| 3 |
∵PE⊥平面ADP,∴平面ADP的法向量为
| n |
| EP |
| 3 |
设M是线段PF上一点,则存在0≤λ≤1,
使
| PM |
| PF |
| DM |
| DP |
| PM |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
.cos<
| n |
| DM |
| ||||
|
|
| 4λ | ||
|
那么|cos<
| n |
| DM |
| 4λ | ||
|
| 1 |
| 2 |
| 16 |
| 13 |
∵此方程在[0,1]内无解,
∴在线段PF上不存在一点M,使DM与平在ADP所成的角为30°.
点评:本题考查用向量法证明线面垂直,求两异面直线所成的角,验证是否存在一点M使得DM与平在ADP所成的角为30°的问题,用向量法解决此类问题大大降低了解题难度,是解此类题的一个优先扶把思路.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目


 (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.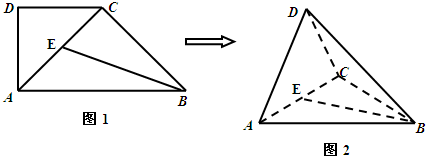 (1)求证:DA⊥BC;
(1)求证:DA⊥BC;