题目内容
 如图,在直角梯形ABCD中,AD⊥AB,BC⊥AB,AD=3,AB=4,BC=
如图,在直角梯形ABCD中,AD⊥AB,BC⊥AB,AD=3,AB=4,BC=| 3 |
(1)建立适当的直角坐标系,求曲线段DE的方程;
(2)试问:过点C能否作一条直线l与曲线段DE相交于两点M、N,使得线段MN以C为中点?若能,则求直线l的方程;
若不能,则说明理由.
分析:(1)以直线AB为x轴,线段AB的中点为原点,建立平面直角坐标系,由AD+BD=3+5=8>AB,知曲线段DE是以A、B为左、右焦点,长轴长为8的椭圆的一部分.由此能求出曲线段DE的方程.
(2)设这样的直线l存在,由直线x=2与曲线段DE只有一个交点(0,3),设直线l的方程为 y=k(x-2)+
,将其代入
+
=1得(3+4k2)x2+(8
k-16k2)x+16k2-16
k-36=0.由此能求出直线l的方程.
(2)设这样的直线l存在,由直线x=2与曲线段DE只有一个交点(0,3),设直线l的方程为 y=k(x-2)+
| 3 |
| x2 |
| 16 |
| y2 |
| 12 |
| 3 |
| 3 |
解答: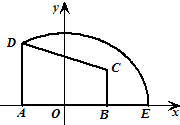 解:(1)以直线AB为x轴,线段AB的中点为原点,
解:(1)以直线AB为x轴,线段AB的中点为原点,
建立如图所示的平面直角坐标系,
则A(-2,0),B(2,0),C(2,
),D(-2,3).…(1分)
∵AD+BD=3+5=8>AB,
∴依题意,曲线段DE是以A、B为左、右焦点,
长轴长为8的椭圆的一部分. (3分)
故曲线段DE的方程为
+
=1(x≥-2,y≥0). (6分)
(2)设这样的直线l存在,
由直线x=2与曲线段DE只有一个交点(0,3),
知直线l存在斜率,设直线l的方程为y-
=k(x-2),
即 y=k(x-2)+
,
将其代入
+
=1,
得(3+4k2)x2+(8
k-16k2)x+16k2-16
k-36=0①(9分)
设M(x1,y1),N(x2,y2),
则由
=2,知x1+x2=4,
∴-
=4,
解得k=-
.(12分)
当k=-
时,方程①化为:x2-4x=0,
解得x1=0,x2=4.
即M(0,2
),N(4,0),适合条件.
故直线l存在,其方程为y=-
x+2
,
即
x+2y-4
=0.(14分)
 解:(1)以直线AB为x轴,线段AB的中点为原点,
解:(1)以直线AB为x轴,线段AB的中点为原点,建立如图所示的平面直角坐标系,
则A(-2,0),B(2,0),C(2,
| 3 |
∵AD+BD=3+5=8>AB,
∴依题意,曲线段DE是以A、B为左、右焦点,
长轴长为8的椭圆的一部分. (3分)
故曲线段DE的方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)设这样的直线l存在,
由直线x=2与曲线段DE只有一个交点(0,3),
知直线l存在斜率,设直线l的方程为y-
| 3 |
即 y=k(x-2)+
| 3 |
将其代入
| x2 |
| 16 |
| y2 |
| 12 |
得(3+4k2)x2+(8
| 3 |
| 3 |
设M(x1,y1),N(x2,y2),
则由
| x1+x2 |
| 2 |
∴-
8
| ||
| 3+4k2 |
解得k=-
| ||
| 2 |
当k=-
| ||
| 2 |
解得x1=0,x2=4.
即M(0,2
| 3 |
故直线l存在,其方程为y=-
| ||
| 2 |
| 3 |
即
| 3 |
| 3 |
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则