Question

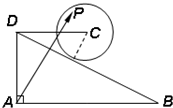（2012•洛阳模拟）如图，在直角梯形ABCD中，AD⊥AB，AB∥DC，AD=DC=1，AB=2，动点P在以点C为圆心，且与直线BD相切的圆上或圆内移动，设

AP

=λ

AD

+μ

AB

（λ，μ∈R），则λ+μ取值范围是（　　）

A．[1，2]

B．[2，4]

C．[2，+∞）

D．（-∞，1]

Answer 1

分析：建立直角坐标系，写出点的坐标，求出BD的方程，求出圆的方程；设出P的坐标，求出三个向量的坐标，将P的坐标用λ，μ表示，代入圆内方程求出范围．

解答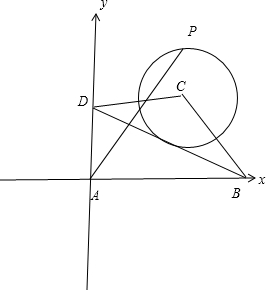：解：以A为坐标原点，AB为x轴，DA为y轴建立平面直角坐标系则
A（0，0），D（0，1），C（1，1），B（2，0）
直线BD的方程为x+2y-2=0，C到BD的距离d=

|1+2-2|

5

=

5

5

∴以点C为圆心，且与直线BD相切的圆方程为（x-2）²+（y-1）²=

1

5

设P（x，y）则

AP

=（x，y），

AD

=（0，1），

AB

=（2，0）
∴（x，y）=（2μ，λ）
∴x=2μ，y=λ
∵P在圆内或圆上
∴（2μ-1）²+（λ-1）²≤

1

5

∴20（μ-

1

2

）²+5（λ-1）²≤1
∴μ-

1

2

≤

1 20

解得1≤λ+μ≤2

点评：通过建立直角坐标系将问题代数化、考查直线与圆相切的条件、考查向量的坐标公式．