题目内容
在直角梯形ACBD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=2,M为腰BC的中点,则
•
=( )
| MA |
| MD |
| A、1 | B、2 | C、3 | D、4 |
分析:以直角梯形的两个直角边为坐标轴,写出点的坐标,求出向量的坐标,利用向量数量积的坐标形式的公式求.
解答:解:以A为原点,AB为x轴,AD为y轴,建立直角坐标系.
则:A(0,0),B(2,0),D(0,1),C(1,1),M(
,
).
因为AB=2CD=2,∠B=45,所以AD=DC=1,M为腰BC的中点,
则M点到AD的距离=
(DC+AB)=
,M点到AB的距离=
DA=
所以
=(-
, -
),
=( -
,
),
所以
•
=9/4-1/4=2.
故答案为B
则:A(0,0),B(2,0),D(0,1),C(1,1),M(
| 3 |
| 2 |
| 1 |
| 2 |
因为AB=2CD=2,∠B=45,所以AD=DC=1,M为腰BC的中点,
则M点到AD的距离=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以
| MA |
| 3 |
| 2 |
| 1 |
| 2 |
| MD |
| 3 |
| 2 |
| 1 |
| 2 |
所以
| MA |
| MD |
故答案为B
点评:本题考查通过建立直角坐标系将几何问题问题转化为代数问题;考查向量的坐标形式的数量积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
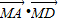 =( )
=( ) =( )
=( )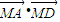 =( )
=( )