变式:如图.四棱锥P―ABCD中.底面ABCD 为矩形.AB=8.AD=4.侧面PAD为等边三角形.并且与底面所成二面角为60°.(Ⅰ)求四棱锥P―ABCD的体积,(Ⅱ)证明PA⊥BD. 解析:(Ⅰ)——青夏教育精英家教网——

摘要：变式:如图.四棱锥P―ABCD中.底面ABCD 为矩形.AB=8.AD=4.侧面PAD为等边三角形.并且与底面所成二面角为60°.(Ⅰ)求四棱锥P―ABCD的体积,(Ⅱ)证明PA⊥BD. 解析:(Ⅰ)如图.取AD的中点E.连结PE.则PE⊥AD.作PO⊥平面在ABCD.垂足为O.连结OE.根据三垂线定理的逆定理得OE⊥AD.所以∠PEO为侧面PAD与底面所成的二面角

网址：http://m.1010jiajiao.com/timu_id_528963[举报]

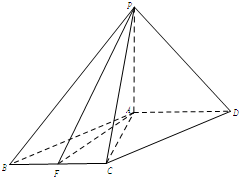（2012•顺义区二模）如图，四棱锥P-ABCD中，底面ABCD是平行四边形，∠ACB=90°，PA⊥平面ABCD，PA=BC=1，AB=

，F是BC的中点．
（Ⅰ）求证：DA⊥平面PAC；
（Ⅱ）试在线段PD上确定一点G，使CG∥平面PAF，并求三棱锥A-CDG的体积．

查看习题详情和答案>>

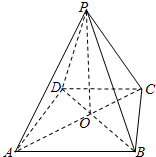如图，四棱锥P-ABCD中，底面ABCD为等腰梯形，AB∥DC，AC⊥BD，O为AC，BD的交点，且PO⊥底面ABCD，OB=2，OD=1，OP=

．
（Ⅰ）求异面直线PD与BC所成角的余弦值；
（Ⅱ）求二面角P-AB-C的大小；
（Ⅲ）设点M在棱PC上，

=λ，问λ为何值时，PC⊥平面BMD．

查看习题详情和答案>>

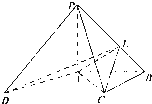如图，四棱锥P-ABCD中，底面ABCD为梯形，AB∥CD，AB⊥BC，PC⊥AD，PA⊥底面ABCD，PA=AB=BC，点E在棱PB上，且PD∥平面EAC．
（I）求证：PE=2EB；
（II）求二面角E-AD-C的大小．查看习题详情和答案>>

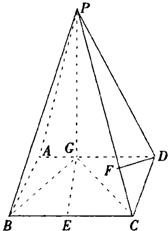如图，四棱锥P-ABCD中，底面ABCD是平行四边形，P在平面ABCD上的射影为G，且G在AD上，且AG=

GD，BG⊥GC，GB=GC=2，E是BC的中点，四面体P-BCG的体积为

．
（Ⅰ）求异面直线GE与PC所成的角余弦值；
（Ⅱ）求点D到平面PBG的距离；
（Ⅲ）若F点是棱PC上一点，且DF⊥GC，求

的值．查看习题详情和答案>>

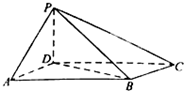如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．
（Ⅰ）证明：PA⊥BD；
（Ⅱ）若PD=AD，求二面角A-PB-C的余弦值．查看习题详情和答案>>