题目内容
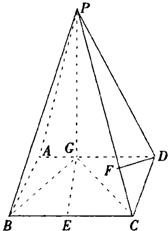 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,P在平面ABCD上的射影为G,且G在AD上,且AG=
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,P在平面ABCD上的射影为G,且G在AD上,且AG=| 1 |
| 3 |
| 8 |
| 3 |
(Ⅰ)求异面直线GE与PC所成的角余弦值;
(Ⅱ)求点D到平面PBG的距离;
(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求
| PF |
| FC |
分析:(1)先利用等体积法求出PG的长,在平面ABCD内,过C点作CH∥EG交AD于H,连接PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角,在△PCH中利用余弦定理求出此角即可;
(2)在平面ABCD内,过D作DK⊥BG,交BG延长线于K,则DK⊥平面PBG,DK的长就是点D到平面PBG的距离,在△DKG利用边角关系求出DK长;
(3)在平面ABCD内,过D作DM⊥GC,M为垂足,连接MF,先证明FM∥PG,然后利用三角形相似对应边成比例建立等量关系即可.
(2)在平面ABCD内,过D作DK⊥BG,交BG延长线于K,则DK⊥平面PBG,DK的长就是点D到平面PBG的距离,在△DKG利用边角关系求出DK长;
(3)在平面ABCD内,过D作DM⊥GC,M为垂足,连接MF,先证明FM∥PG,然后利用三角形相似对应边成比例建立等量关系即可.
解答: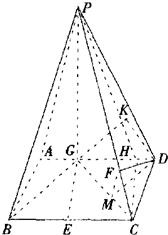 解:(I)由已知VP-BGC=
解:(I)由已知VP-BGC=
S△BCG•PG=
•
BG•GC•PG=
,
∴PG=4.
在平面ABCD内,过C点作CH∥EG交AD于H,连接PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角.
在△PCH中,CH=
,PC=
,PH=
,
由余弦定理得,cos∠PCH=
,
∴异面直线GE与PC所成的角的余弦值为
.
(II)∵PG⊥平面ABCD,PG?平面PBG∴平面PBG⊥平面ABCD,
在平面ABCD内,过D作DK⊥BG,交BG延长线于K,则DK⊥平面PBG∴DK的长就是点D到平面PBG的距离.
∵BC=2
∴GD=
AD=
BC=
.
在△DKG,DK=DGsin45°=
,∴点D到平面PBG的距离为
.
(III)在平面ABCD内,过D作DM⊥GC,M为垂足,连接MF,
又因为DF⊥GC,
∴GC⊥平面MFD,∴GC⊥FM.
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD∴FM∥PG;
由GM⊥MD得:GM=GD•cos45°=
.
∵
=
=
=3,∴由DF⊥GC可得
=3,
∴
x=
,解得d=
∈(0,
).
 解:(I)由已知VP-BGC=
解:(I)由已知VP-BGC=| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
∴PG=4.
在平面ABCD内,过C点作CH∥EG交AD于H,连接PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角.
在△PCH中,CH=
| 2 |
| 20 |
| 18 |
由余弦定理得,cos∠PCH=
| ||
| 10 |
∴异面直线GE与PC所成的角的余弦值为
| ||
| 10 |
(II)∵PG⊥平面ABCD,PG?平面PBG∴平面PBG⊥平面ABCD,
在平面ABCD内,过D作DK⊥BG,交BG延长线于K,则DK⊥平面PBG∴DK的长就是点D到平面PBG的距离.
∵BC=2
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 2 |
在△DKG,DK=DGsin45°=
| 3 |
| 2 |
| 3 |
| 2 |
(III)在平面ABCD内,过D作DM⊥GC,M为垂足,连接MF,
又因为DF⊥GC,
∴GC⊥平面MFD,∴GC⊥FM.
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD∴FM∥PG;
由GM⊥MD得:GM=GD•cos45°=
| 3 |
| 2 |
∵
| PF |
| FC |
| GM |
| MC |
| ||
|
| PF |
| FC |
∴
| ||
| 3 |
| d |
| 3 |
| x2+3 |
| ||
|
| 3 |
点评:本题主要考查四棱锥的有关知识,以及求异面直线所成角的问题,以及分析问题与解决问题的能力.简单几何体是立体几何解答题的主要载体,特别是棱柱和棱锥.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=