题目内容
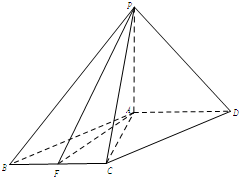 (2012•顺义区二模)如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,PA⊥平面ABCD,PA=BC=1,AB=
(2012•顺义区二模)如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,PA⊥平面ABCD,PA=BC=1,AB=| 2 |
(Ⅰ)求证:DA⊥平面PAC;
(Ⅱ)试在线段PD上确定一点G,使CG∥平面PAF,并求三棱锥A-CDG的体积.
分析:(Ⅰ)平行四边形ABCD中,证出AC⊥DA.结合PA⊥平面ABCD,得PA⊥DA,由线面垂直的判定定理,可得DA⊥平面PAC.
(Ⅱ)设PD的中点为G,在平面PAD内作GH⊥PA于H,连接FH,可证出四边形FCGH为平行四边形,得GC∥FH,所以CG∥平面PAF.设点G到平面ABCD的距离为d,得d=
PA=
,结合Rt△ACD面积和锥体体积公式,可算出三棱锥A-CDG的体积.
(Ⅱ)设PD的中点为G,在平面PAD内作GH⊥PA于H,连接FH,可证出四边形FCGH为平行四边形,得GC∥FH,所以CG∥平面PAF.设点G到平面ABCD的距离为d,得d=
| 1 |
| 2 |
| 1 |
| 2 |
解答: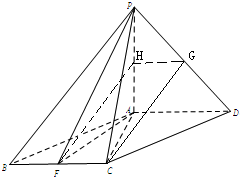 解:(Ⅰ)∵四边形是平行四边形,
解:(Ⅰ)∵四边形是平行四边形,
∴AD∥BC,可得∠ACB=∠DAC=90°,即AC⊥DA
∵PA⊥平面ABCD,DA⊆平面ABCD,∴PA⊥DA,
又∵AC⊥DA,AC∩PA=A,∴DA⊥平面PAC.
(Ⅱ)设PD的中点为G,在平面PAD内作GH⊥PA于H,连接FH,
则△PAD中,GH平行且等于
AD
∵平行四边形ABCD中,FC平行且等于
AD,
∴GH∥FC且GH=FC,四边形FCGH为平行四边形,得GC∥FH,
∵FH?平面PAF,CG?平面PAF,
∴CG∥平面PAF,即G为PD中点时,CG∥平面PAF.
设点G到平面ABCD的距离为d,则
由G为PD中点且PA⊥平面ABCD,得d=
PA=
,
又∵Rt△ACD面积为
×1×1=
∴三棱锥A-CDG的体积VA-CDG=VG-CDA=
S△ACD×
=
.
 解:(Ⅰ)∵四边形是平行四边形,
解:(Ⅰ)∵四边形是平行四边形,∴AD∥BC,可得∠ACB=∠DAC=90°,即AC⊥DA
∵PA⊥平面ABCD,DA⊆平面ABCD,∴PA⊥DA,
又∵AC⊥DA,AC∩PA=A,∴DA⊥平面PAC.
(Ⅱ)设PD的中点为G,在平面PAD内作GH⊥PA于H,连接FH,
则△PAD中,GH平行且等于
| 1 |
| 2 |
∵平行四边形ABCD中,FC平行且等于
| 1 |
| 2 |
∴GH∥FC且GH=FC,四边形FCGH为平行四边形,得GC∥FH,
∵FH?平面PAF,CG?平面PAF,
∴CG∥平面PAF,即G为PD中点时,CG∥平面PAF.
设点G到平面ABCD的距离为d,则
由G为PD中点且PA⊥平面ABCD,得d=
| 1 |
| 2 |
| 1 |
| 2 |
又∵Rt△ACD面积为
| 1 |
| 2 |
| 1 |
| 2 |
∴三棱锥A-CDG的体积VA-CDG=VG-CDA=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 12 |
点评:本题给出四棱锥,求证线面垂直并求锥体的体积,着重考查了线面垂直的判定与性质、线面平行的判定和锥体体积公式等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•顺义区二模)如图是一个空间几何体的三视图,则该几何体的体积为( )
(2012•顺义区二模)如图是一个空间几何体的三视图,则该几何体的体积为( )