题目内容
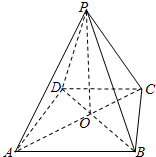 如图,四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥DC,AC⊥BD,O为AC,BD的交点,且PO⊥底面ABCD,OB=2,OD=1,OP=
如图,四棱锥P-ABCD中,底面ABCD为等腰梯形,AB∥DC,AC⊥BD,O为AC,BD的交点,且PO⊥底面ABCD,OB=2,OD=1,OP=| 2 |
(Ⅰ)求异面直线PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)设点M在棱PC上,
| PM |
| MC |
分析:(Ⅰ)由题设CD=
,AB=2
,BC=
,取AB中点E,连接DE,PE,则有四边形BCDE为平行四边形,则BC∥DE,故∠PDE为异面直线PD与BC所成角(或其补角),由此能求出异面直线PD与BC所成角的余弦值.
(Ⅱ)连接OE,则OE⊥AB,AB⊥平面POE,所以∠PEO即为所求二面角的平面角,由此能求出二面角P-AB-C的大小.
(Ⅲ)连接OM,由题设,PC⊥BD,若PC⊥平面BMD,只须PC⊥OM即可,由此能求出λ的值.
| 2 |
| 2 |
| 5 |
(Ⅱ)连接OE,则OE⊥AB,AB⊥平面POE,所以∠PEO即为所求二面角的平面角,由此能求出二面角P-AB-C的大小.
(Ⅲ)连接OM,由题设,PC⊥BD,若PC⊥平面BMD,只须PC⊥OM即可,由此能求出λ的值.
解答: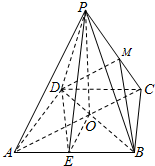 (本小题13分)
(本小题13分)
解:(Ⅰ)∵底面ABCD为等腰梯形,AB∥DC,AC⊥BD,
O为AC,BD的交点,且PO⊥底面ABCD,OB=2,OD=1,OP=
.
∴CD=
,AB=2
,BC=
,取AB中点E,
连接DE,PE,则有四边形BCDE为平行四边形,
则BC∥DE
故∠PDE为异面直线PD与BC所成角(或其补角)…(3分)
又PD=
,DE=
,PE=2,
由余弦定理求得:
cos∠PDE=
=
…(5分)
(Ⅱ)连接OE,则OE⊥AB,AB⊥平面POE,
∴∠PEO即为所求二面角的平面角,
∵BE=
,BO=2,OE⊥AB,
∴OE=
=
,
∴∠PEO=45°…(9分)
(Ⅲ)连接OM,由题设,PC⊥BD,
若PC⊥平面BMD,只须PC⊥OM即可,
在Rt△POC中,PM=
=
=
PC,
∴λ=2…(13分).
 (本小题13分)
(本小题13分)解:(Ⅰ)∵底面ABCD为等腰梯形,AB∥DC,AC⊥BD,
O为AC,BD的交点,且PO⊥底面ABCD,OB=2,OD=1,OP=
| 2 |
∴CD=
| 2 |
| 2 |
| 5 |
连接DE,PE,则有四边形BCDE为平行四边形,
则BC∥DE
故∠PDE为异面直线PD与BC所成角(或其补角)…(3分)
又PD=
| 3 |
| 5 |
由余弦定理求得:
cos∠PDE=
| PD2+DE2-PE2 |
| 2PD•DE |
| 2 |
| 15 |
| 15 |
(Ⅱ)连接OE,则OE⊥AB,AB⊥平面POE,
∴∠PEO即为所求二面角的平面角,
∵BE=
| 2 |
∴OE=
| 4-2 |
| 2 |
∴∠PEO=45°…(9分)
(Ⅲ)连接OM,由题设,PC⊥BD,
若PC⊥平面BMD,只须PC⊥OM即可,
在Rt△POC中,PM=
| PO2 |
| PC |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
∴λ=2…(13分).
点评:本题考查异面直线所成角的余弦值的求法,考查二面角的求法,考查满足条件的实数值的求法.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=