0 53721 53729 53735 53739 53745 53747 53751 53757 53759 53765 53771 53775 53777 53781 53787 53789 53795 53799 53801 53805 53807 53811 53813 53815 53816 53817 53819 53820 53821 53823 53825 53829 53831 53835 53837 53841 53847 53849 53855 53859 53861 53865 53871 53877 53879 53885 53889 53891 53897 53901 53907 53915 447348
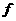 (x)在
(x)在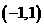 上有定义,
上有定义,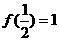 ,且满足
,且满足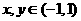 时有
时有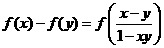 ,对数列
,对数列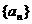 满足
满足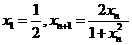
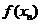 的表达式;
的表达式;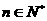 ,有
,有 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值.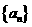 的首项
的首项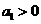 ,公比
,公比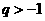 且
且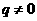 的等比数列,设数列
的等比数列,设数列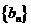 的通项
的通项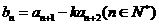 ,数列
,数列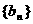 的前n项之和分别为
的前n项之和分别为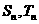 ,如果存在常数k,使得对所有的适合条件的两个数列,均有
,如果存在常数k,使得对所有的适合条件的两个数列,均有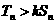 对一切
对一切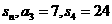 。
。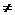 q,证明
q,证明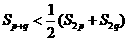
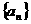 满足条件
满足条件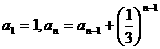
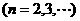
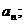 (2)求
(2)求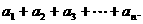
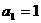 ,
,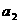 ,
,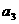 ,…法则如下:如果
,…法则如下:如果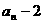 为自然数且未写出过,则写
为自然数且未写出过,则写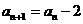 ,否则就写
,否则就写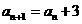 ,那么
,那么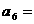
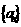 是等差数列.则通项为
是等差数列.则通项为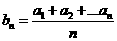 的数列
的数列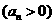 ,则通项为
,则通项为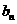 =_____________的数列
=_____________的数列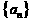 的前
的前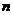 项和为
项和为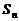 (
(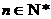 ). 关于数列
). 关于数列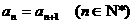 ;
;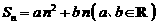 ,则
,则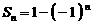 ,则
,则