摘要:若函数()的最小正周期为. (I)求的值, (II)求函数在区间上的取值范围. 某车站每天8∶00~9∶00.9∶00~10∶00都恰有一辆客车到站.各车到站时刻是随机的.且各车到站的时间相互独立.其规律为 到站时刻 8∶10 8∶30 8∶50 9∶10 9∶30 9∶50 概率 一旅客8∶20到车站.求: (I) 该旅客9点之前乘上车的概率, (II) 该旅客候车时间超过1小时的概率. 在长方体ABCD-A1B1C1D1中.已知AB=BC=2.BB1=3.连接BC1.过B1作B1E⊥BC1 交CC1于点E (I)求证:AC1⊥平面B1D1E, (II)求二面角E-B1D1-C1的平面角大小 已知函数f(x)=x3+ax2+bx+c在时取得极值,在点的切线斜率为4. (I)求a.b的值与函数f(x)的单调区间 (II)若对xÎ[-1.2].不等式f(x)< 恒成立.求c的取值范围. 椭圆过点P.且离心率为. F为椭圆的右焦点.过F作直线交椭圆C于M.N两点.定点A(). (I)求椭圆C的方程, (II)当 =3时, 求直线MN的方程. 已知等差数列{an}前三项为a.4.3a.前n项和为Sn. (I)求a及{an}的通项公式, (II)若Sk = 2550.求k的值, (III)求证: -<1.
网址:http://m.1010jiajiao.com/timu3_id_534647[举报]
 在
在 处取得最值.
处取得最值.  的最小正周期及
的最小正周期及 的值;
的值; 是首项与公差均为
是首项与公差均为 的等差数列,求
的等差数列,求 的值.
的值.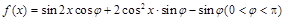 在
在 处取得最值.
处取得最值. 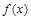 的最小正周期及
的最小正周期及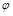 的值;
的值;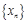 是首项与公差均为
是首项与公差均为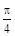 的等差数列,求
的等差数列,求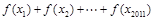 的值.
的值.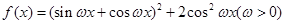 的最小正周期为
的最小正周期为 .
.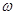 的值.
的值.  的图像是由
的图像是由 的图像向右平移
的图像向右平移 个单位长度得到,求
个单位长度得到,求 满分13分)
满分13分)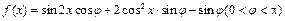 在
在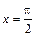 处取得最值.
处取得最值. 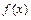 的最小正周期及
的最小正周期及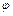 的值;
的值;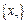 是首项与公差均为
是首项与公差均为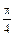 的等差数列,求
的等差数列,求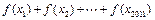 的值.
的值.