网址:http://m.1010jiajiao.com/timu3_id_534543[举报]
(本小题满分14分)
已知函数f(x)=![]() ,g(x)=alnx,a
,g(x)=alnx,a![]() R。
R。
若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
设函数h(x)=f(x)- g(x),当h(x)存在最小之时,求其最小值![]() (a)的解析式;
(a)的解析式;
对(2)中的![]() (a),证明:当a
(a),证明:当a![]() (0,+
(0,+![]() )时,
)时, ![]() (a)
(a)![]() 1.
1.
(本小题满分14分)
已知函数f(x)=![]() ,g(x)=alnx,a
,g(x)=alnx,a![]() R。
R。
若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
设函数h(x)=f(x)- g(x),当h(x)存在最小之时,求其最小值![]() (a)的解析式;
(a)的解析式;
对(2)中的![]() (a),证明:当a
(a),证明:当a![]() (0,+
(0,+![]() )时,
)时, ![]() (a)
(a)![]() 1.
1.
(本小题满分14分)
为积极响应国家“家电下乡”政策的号召,某厂家把总价值为10万元的A、B两种型号的电视机投放市场,并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元,农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴,补贴方案如下表所示,设投放市场的A、B型号电视机的价值分别为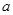 万元,
万元,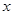 万元,农民得到的补贴为
万元,农民得到的补贴为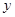 万元,解答以下问题.
万元,解答以下问题.
|
|
A型号 |
B型号 |
|
电视机价值(万元) |
|
|
|
农民获得补贴(万元) |
|
|
(1) 用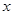 的代数式表示
的代数式表示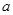
(2) 当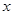 取何值时,
取何值时, 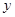 取最大值并求出其最大值(精确到0.1,参考数据:
取最大值并求出其最大值(精确到0.1,参考数据: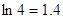 )
)
查看习题详情和答案>>
(本小题满分14分)
为积极响应国家“家电下乡”政策的号召,某厂家把总价值为10万元的A、B两种型号的电视机投放市场,并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元,农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴,补贴方案如下表所示,设投放市场的A、B型号电视机的价值分别为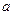 万元,
万元,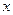 万元,农民得到的补贴为
万元,农民得到的补贴为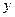 万元,解答以下问题.
万元,解答以下问题.
| | A型号 | B型号 |
| 电视机价值(万元) | 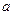 | 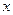 |
| 农民获得补贴(万元) | 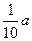 |  |
(1) 用
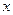 的代数式表示
的代数式表示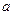
(2) 当
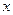 取何值时,
取何值时, 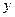 取最大值并求出其最大值(精确到0.1,参考数据:
取最大值并求出其最大值(精确到0.1,参考数据: )
查看习题详情和答案>>
)
查看习题详情和答案>>
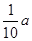
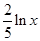
 万元,
万元,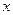 万元,农民得到的补贴为
万元,农民得到的补贴为 万元,解答以下问题.
万元,解答以下问题.

 )
)