17 (12分)
 已知
已知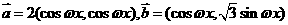
(其中0< <1),函数
<1),函数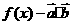 若直线
若直线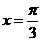 是
是
函数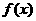 图像的一条对称轴,
图像的一条对称轴,
(I)
试求 的值;
的值;
(II)
先列表在作出函数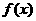 在区间
在区间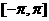 上的图像
上的图像
18 (12分)
某研究机构准备举办一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(I) 从这50名教师中随机选出2名,问这2人使用相同版本教材的概率是多少?
(II) 现从这50名教师中随机选出2名教师做问卷调查,若选出3名教师都使用人教版教材,求恰有1人使用人教版A版的概率是多少?
(III)
若随机选出的2名教师都是用人教版教材,设其中使用人教A版教材的教师人数为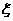 的分布列和数学期望。
的分布列和数学期望。
19 (12分)
如图,已知里棱锥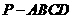 的底面为直角梯形,
的底面为直角梯形,
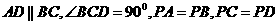
(I)
 证明平面
证明平面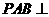 平面ABCD;
平面ABCD;
(II)
如果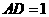
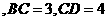 ,且侧面
,且侧面 的面积为8,求四棱锥
的面积为8,求四棱锥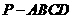 的面积。
的面积。
20 (12分)
已知函数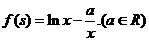
(I)
讨论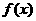 在
在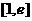 上的单调性;
上的单调性;
(II)
若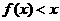 在
在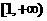 上恒成立,试求
上恒成立,试求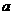 的取值范围。
的取值范围。
21(12分)
已知数列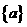 满足
满足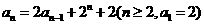 ,
,
(I)
求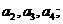
(II)
是否存在一个实数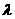 ,使得数列
,使得数列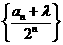 成等差数列,若存在,求出
成等差数列,若存在,求出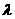 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(III)
求数列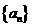 的前n项和,证明:
的前n项和,证明: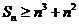
22 (14分)
已知中心在原点、焦点在x轴上的椭圆,其离心率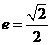 ,且经过抛物线
,且经过抛物线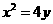 的焦点。
的焦点。
(I) 求椭圆的标准方程;
(II)
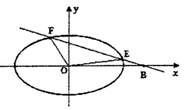 若过点B(2,0)的直线l与椭圆交于不同的亮点E、F(E在B、F之间)且
若过点B(2,0)的直线l与椭圆交于不同的亮点E、F(E在B、F之间)且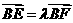 ,试求实数
,试求实数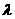 的取值范围。
的取值范围。
淄博市2008-2009学年度高三模拟考试
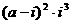 为纯虚数,则实数
为纯虚数,则实数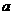 等于 ( )
等于 ( )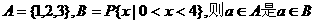 的 ( )
的 ( )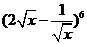 展开式中韩x2项的系数是
。
展开式中韩x2项的系数是
。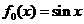 ,则输出的是
,则输出的是
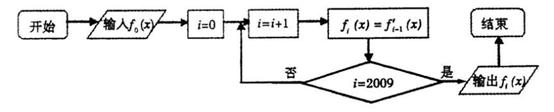
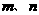 是不同的直线,
是不同的直线,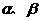 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题: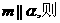 m平行与平面
m平行与平面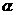 内的无数条直线
内的无数条直线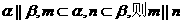
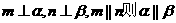
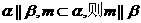
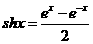 和双曲线余弦函数
和双曲线余弦函数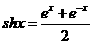 ,而双曲线正弦函数和双曲线余弦函数与我们学过的正弦函数和余弦函数有关类似的性质,比如关于正、余弦函数有
,而双曲线正弦函数和双曲线余弦函数与我们学过的正弦函数和余弦函数有关类似的性质,比如关于正、余弦函数有 成立,而关于双曲正、余弦函数满足
成立,而关于双曲正、余弦函数满足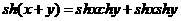 。请你御用类比的思想,写出关于双曲正弦、双曲余弦很熟的一个新关系试
。请你御用类比的思想,写出关于双曲正弦、双曲余弦很熟的一个新关系试
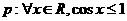 则
则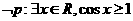 B
B 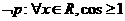
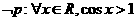 D
D 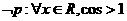
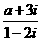 (
(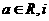 为虚数单位)是纯虚数,则实数
为虚数单位)是纯虚数,则实数
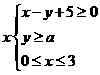 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则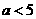 B
B
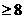 C
C
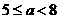 D
D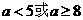
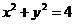 相交于A、B两点,则|AB|的最小值为
相交于A、B两点,则|AB|的最小值为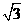 C 3
D2
C 3
D2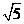
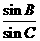 的值为
的值为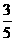 B
B
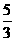 C
C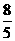 D
D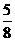
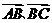 和
和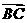 满足
满足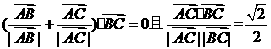 ,则
,则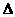 ABC为
ABC为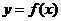 的图像如图所示,则函数
的图像如图所示,则函数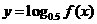 的图像大致是
的图像大致是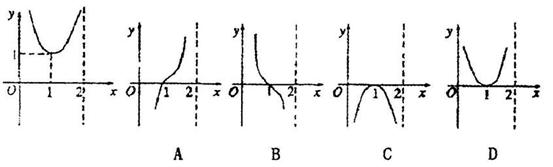
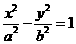 的一条渐近线的距离为
的一条渐近线的距离为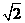 ,则在双曲线德离心率为
,则在双曲线德离心率为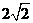 D
D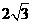
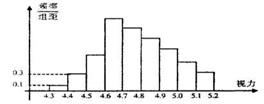 11 为了解某校高三学生的视力情况,随机地抽查了
11 为了解某校高三学生的视力情况,随机地抽查了 的值分别为
的值分别为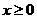 时
时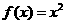 ,若对任意的
,若对任意的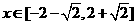 不等式
不等式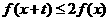 恒成立,则实数t的取值范围是
恒成立,则实数t的取值范围是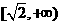 B
B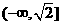
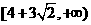 D
D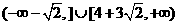
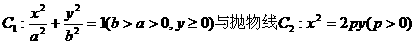 的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为
的交点分别为A,B,曲线C1与抛物线C2在点A处的切线分别为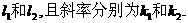
 无关?若是,给出证明;若否,给以说明;
无关?若是,给出证明;若否,给以说明;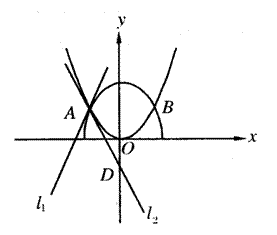 (II)若
(II)若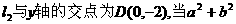 取得最小值9时,求曲线C1与抛物线C2的方程。
取得最小值9时,求曲线C1与抛物线C2的方程。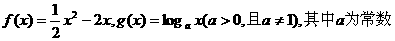 ,如果
,如果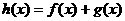 在其定义域上是增函数,且
在其定义域上是增函数,且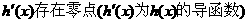 。
。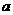 的值;
的值;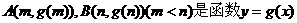 的图象上两点,
的图象上两点,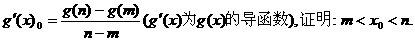
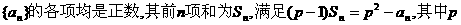 为正常数,且
为正常数,且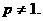
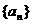 的通项公式;
的通项公式;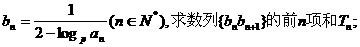
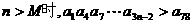 恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。
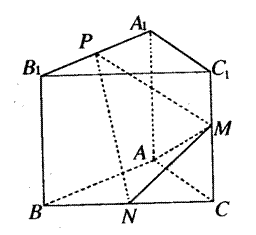
恒成立?若存在,求出相应的M的最小值;若不存在,请说明理由。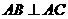 ,M是CC1的中点,N是BC的中点,点P在A1B1上,且满足
,M是CC1的中点,N是BC的中点,点P在A1B1上,且满足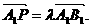
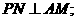
 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角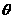 最大?并求该角最大值的正切值;
最大?并求该角最大值的正切值;