0 51841 51849 51855 51859 51865 51867 51871 51877 51879 51885 51891 51895 51897 51901 51907 51909 51915 51919 51921 51925 51927 51931 51933 51935 51936 51937 51939 51940 51941 51943 51945 51949 51951 51955 51957 51961 51967 51969 51975 51979 51981 51985 51991 51997 51999 52005 52009 52011 52017 52021 52027 52035 447348
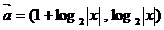 ,
,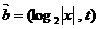
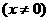 .
.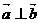 ,求实数x的值;
,求实数x的值;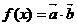 具备的性质.
具备的性质.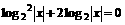 ……2分
……2分 ……4分
……4分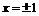 ,或
,或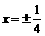 ……6分
……6分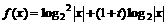 ……8分
……8分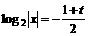 即
即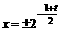 时,
时,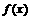 取得最小值
取得最小值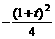 (写出值域为
(写出值域为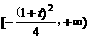 也可);
也可);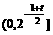 上递减,
上递减,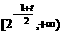 上递增;由对称性,在
上递增;由对称性,在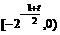 上递增,在
上递增,在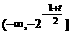 递减
……14分
递减
……14分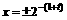 )等皆可。写出函数的定义域不得分,写错扣1分
)等皆可。写出函数的定义域不得分,写错扣1分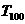 = 991 。
= 991 。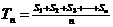 为数列{an}的“凯森和”,
为数列{an}的“凯森和”, 
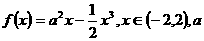 为正常数。
为正常数。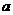 、
、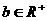 ,则
,则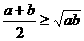 (当且仅当
(当且仅当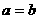 时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);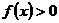 在
在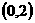 上恒成立,且函数
上恒成立,且函数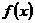 的最大值大于
的最大值大于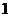 ,求实数
,求实数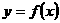 的单调性(无需证明);
的单调性(无需证明);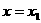 时,
时,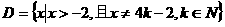 上的函数
上的函数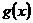 ,使当
,使当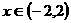 时,
时,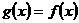 ,当
,当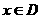 时,
时,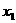 为首项的等差数列。
为首项的等差数列。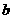 、
、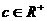 ,则
,则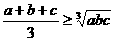 (当且仅当
(当且仅当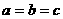 时取等号)。
时取等号)。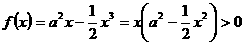 在
在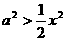 在
在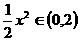 ,∴
,∴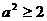 ,即
,即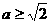 ,
,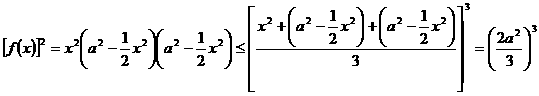 ∴
∴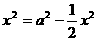 ,即
,即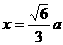 时,
时,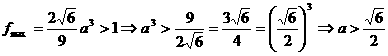 ,
,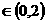 ,∴
,∴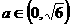 。
综上,得
。
综上,得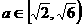 。
。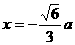 时,函数有最小值。
时,函数有最小值。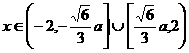 时,
时,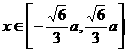 时,
时,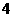 为周期的周期函数即可。
为周期的周期函数即可。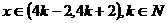 ,
,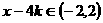 ,此时
,此时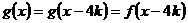 ,
,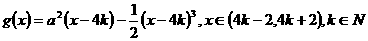 。
。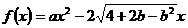 ,
,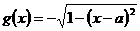 ,
,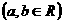
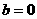 时,若
时,若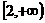 上单调递增,求
上单调递增,求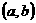 :当
:当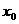 ,使得
,使得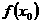 是
是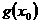 是
是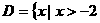 ,且
,且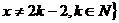 上的函数
上的函数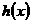 ,使当
,使当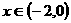 时,
时,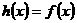 ,当
,当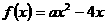 ,
,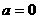 ,
,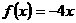 ,则
,则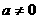 ,要使
,要使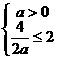 ,∴
,∴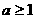 。
。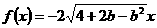 ,则
,则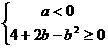 ,即
,即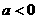 且
且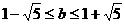 ,
,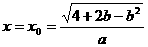 时,
时,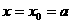 ,依题意,有
,依题意,有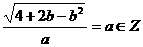 ,则
,则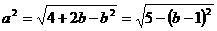 ,
,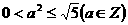 ,得
,得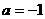 ,此时
,此时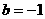 或
或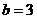 。
。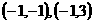 。
。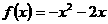
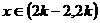 ,
,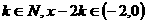 ,
,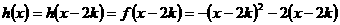 ,
,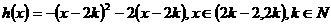 。
。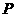 表示幂函数
表示幂函数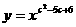 在
在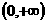 上是增函数的
上是增函数的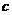 的集合;
的集合;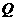 表示不等式
表示不等式 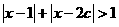 对任意
对任意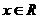 恒成立的
恒成立的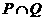 ;(2)试写出一个解集为
;(2)试写出一个解集为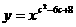 在
在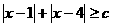 对任意
对任意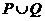 ;(2)试写出一个解集为
;(2)试写出一个解集为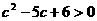 ,即
,即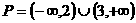 ,
,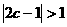 ,即
,即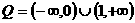 ,
,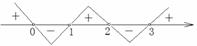 ∴
∴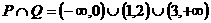 。
。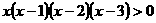 。
。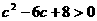 ,即
,即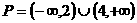 ,
,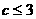 ,即
,即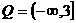 ,
,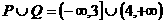 。
。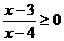 。
。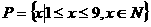 ,记
,记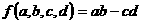 ,(其中
,(其中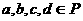 ),例如:
),例如: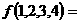
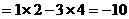 。设
。设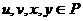 ,且满足
,且满足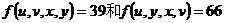 ,则有序数组
,则有序数组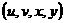
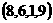 。
。 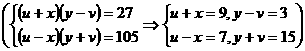
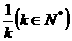 。已知一个铁钉受击
。已知一个铁钉受击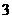 次后全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的
次后全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的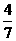 ,请从这个实事中提炼出一个不等式组是
,请从这个实事中提炼出一个不等式组是 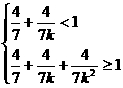 。
。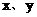 之间满足
之间满足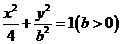
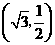 ,求b的值
,求b的值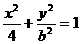 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;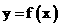 ,如能,求解析式;如不能,再加什么条件就可使
,如能,求解析式;如不能,再加什么条件就可使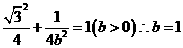 (4分)
(4分)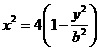 (5分)
(5分)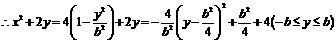 (7分)
(7分)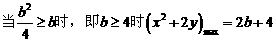
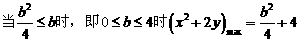
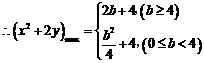 (10分)
(10分)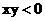 就可使
就可使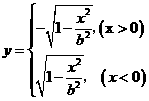 (14分)
(14分)