摘要:(理)已知为正常数. (1)可以证明:定理“若..则(当且仅当时取等号) 推广到三个正数时结论是正确的.试写出推广后的结论, (2)若在上恒成立.且函数的最大值大于.求实数的取值范围.并由此猜测的单调性, 的条件的一个常数.设时.取得最大值.试构造一个定义在上的函数.使当时..当时.取得最大值的自变量的值构成以为首项的等差数列. 解:(1)若...则(当且仅当时取等号). (2)在上恒成立.即在上恒成立. ∵.∴.即. 又∵ ∴.即时. . 又∵.∴. 综上.得 . 易知.是奇函数.∵时.函数有最大值.∴时.函数有最小值. 故猜测:时.单调递减,时.单调递增. (3)依题意.只需构造以为周期的周期函数即可. 如对..此时. 即 . (文)已知函数.. (Ⅰ)当时.若在上单调递增.求的取值范围, (Ⅱ)求满足下列条件的所有实数对:当是整数时.存在.使得是的最大值.是的最小值, 的条件的一个实数对.试构造一个定义在.且上的函数.使当时..当时.取得最大值的自变量的值构成以为首项的等差数列. 解:(Ⅰ)当时.. 若..则在上单调递减.不符题意. 故.要使在上单调递增.必须满足 .∴ . (Ⅱ)若..则无最大值.故.∴为二次函数. 要使有最大值.必须满足.即且. 此时.时.有最大值. 又取最小值时..依题意.有.则. ∵且.∴.得.此时或. ∴满足条件的实数对是. (Ⅲ)当实数对是时. 依题意.只需构造以2为周期的周期函数即可. 如对.. 此时.. 故.
网址:http://m.1010jiajiao.com/timu3_id_519385[举报]
 为正常数。
为正常数。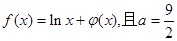 ,求函数
,求函数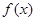 在区间
在区间 上的最大值与最小值
上的最大值与最小值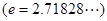 ;
; ,且对任意
,且对任意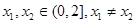 都有
都有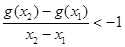 ,求
,求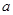 的取值范围。
的取值范围。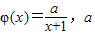 为正常数.(e=2.71828…);
为正常数.(e=2.71828…);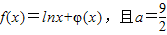 ,求函数f(x)在区间[1,e]上的最大值与最小值
,求函数f(x)在区间[1,e]上的最大值与最小值 ,求a的取值范围.
,求a的取值范围.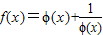 ,求函数f(x)在区间[1,e]上的最大值与最小值.
,求函数f(x)在区间[1,e]上的最大值与最小值. 题满分13分)
题满分13分)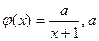 为正常数。
为正常数。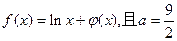 ,求函数
,求函数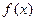
 在区间
在区间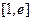 上的最大值与最小值
上的最大值与最小值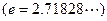 ;
;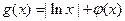 ,且对任意
,且对任意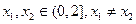 都有
都有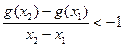 ,求
,求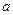 的取值范围。
的取值范围。