0 48259 48267 48273 48277 48283 48285 48289 48295 48297 48303 48309 48313 48315 48319 48325 48327 48333 48337 48339 48343 48345 48349 48351 48353 48354 48355 48357 48358 48359 48361 48363 48367 48369 48373 48375 48379 48385 48387 48393 48397 48399 48403 48409 48415 48417 48423 48427 48429 48435 48439 48445 48453 447348


 ∴得到 c=4
∴得到 c=4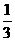 , b=
, b=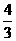 , c=4
, c=4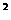 +
+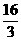 . )
. )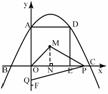 四边形OADE为正方形. --------------------------------------------------------------------------4分
四边形OADE为正方形. --------------------------------------------------------------------------4分 +
+ =
=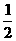 (6-t)×2+
(6-t)×2+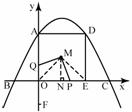 当2<t<6时,连接MO,ME则MO=ME且∠QOM=∠PEM=45
当2<t<6时,连接MO,ME则MO=ME且∠QOM=∠PEM=45 ---------------------------------8分
---------------------------------8分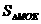 =
=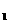 (1,5),N
(1,5),N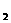 (5,
(5,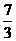 ),N
),N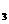 (2+
(2+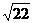 ,-2),N
,-2),N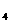 (2-
(2-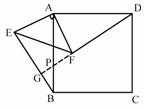 在正方形ABCD和等腰直角△AEF中
在正方形ABCD和等腰直角△AEF中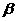 =180°-
=180°-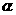 .---------------------------------------------------------------7分
.---------------------------------------------------------------7分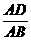 =k,
=k,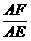 =k
=k 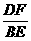 =
=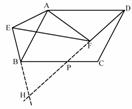 ∵∠AFD+∠AFH=180
∵∠AFD+∠AFH=180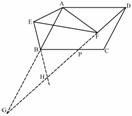 证法(二):DF=kBE的证法与证法(一)相同
证法(二):DF=kBE的证法与证法(一)相同 BHP、
BHP、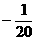 x+85;
x+85;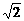 --------------------------------------------------------------------------------------------------5分
--------------------------------------------------------------------------------------------------5分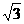
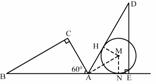 在Rt△AMN中,tan∠MAN=
在Rt△AMN中,tan∠MAN=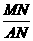 =
=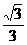 ∴∠MAN=30°---------------------------------------------7分
∴∠MAN=30°---------------------------------------------7分 =
=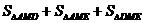 -----------------------------8分
-----------------------------8分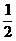 AC·BC=
AC·BC=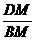 ∴tan60°=
∴tan60°=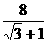 ≈3.0或 x=4(
≈3.0或 x=4(