3、观察下列图形并填表:
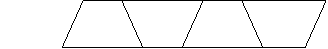
|
梯形个数 |
1 |
2 |
3 |
4 |
5 |
6 |
... |
n |
|
周 长 |
5 |
9 |
13 |
17 |
|
|
... |
|
1、下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.
(1)我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表:(6分)
|
图号 |
顶点数x |
棱数y |
面数z |
|
(a) |
8 |
12 |
6 |
|
(b) |
|
|
|
|
(c) |
|
|
|
|
(d) |
|
|
|
|
(e) |
|
|
|
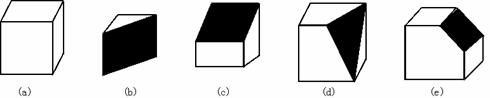
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.(2分)
2如图,已知抛物线L1: y=x2-4的图像与x有交于A、C两点,
(1)若抛物线l2与l1关于x轴对称,求l2的解析式;(3分)
(2)若点B是抛物线l1上的一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点定为D,求证:点D在l2上;(4分)
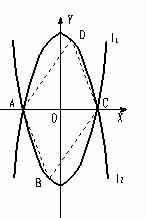 (3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。(4分)
(3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。(4分)
25.(本题满分12分)
如图表示一艘轮船与一艘快艇沿相同路线从甲港到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).根据图象解答下列问题:
(1)请分别求出表示轮船和快艇行驶过程的函数解析式(不要求写出自变量的取值范围);
(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
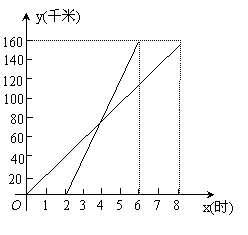 (3)问快艇出发多长时间赶上快艇?
(3)问快艇出发多长时间赶上快艇?
26 (本题满分12分)
(本题满分12分)
图1是棱长为a的小正方体,图2、图3由这样的小正方体摆放而成.按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层的小正方体的个数为s.解答下列问题:
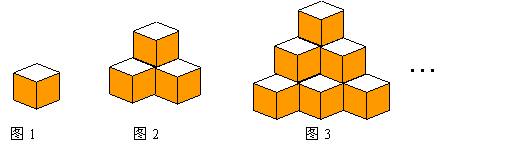
(1)按照要求填表:
|
n |
1 |
2 |
3 |
4 |
… |
|
||||
|
s |
1 |
3 |
6 |
|
… |
|
||||
|
n |
1 |
2 |
3 |
4 |
… |
|
||||
|
s |
1 |
3 |
6 |
|
… |
|
||||
|
n |
1 |
2 |
3 |
4 |
… |
|
||||
|
s |
1 |
3 |
6 |
|
… |
|
||||
|
n |
1 |
2 |
3 |
4 |
… |
|||||
|
s |
1 |
3 |
6 |
|
… |
|||||
|
n |
1 |
2 |
3 |
4 |
… |
|
s |
1 |
3 |
6 |
|
… |
|
n |
1 |
2 |
3 |
4 |
… |
|
s |
1 |
3 |
6 |
|
… |
(2)写出当n=10时,s= .
(3)根据上表中的数据,把s作为纵坐标,n作为横坐标,在平面直角坐标系中描出相应的各点.
(4)请你猜一猜上述各点会在某一函数图象上吗?如果在某一函数图象上,求出该函数的解析式;如果不在某一函数图象上,说明理由.
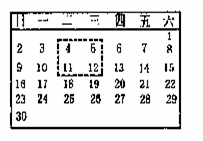 如图是2002年6月份的日历,现有一矩形在日历任意框出4个数
如图是2002年6月份的日历,现有一矩形在日历任意框出4个数 ,请用一个等式表示a、b、c、d之间的关系:__________.
,请用一个等式表示a、b、c、d之间的关系:__________.
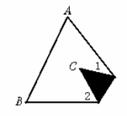 若∠1=20°,则∠2的度数为______.
若∠1=20°,则∠2的度数为______.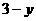 与
与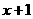 成反比例,且当改造经费投入1万元时,今年的年产量是2万只.
成反比例,且当改造经费投入1万元时,今年的年产量是2万只.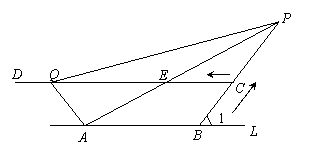 当QE恰好平分△APQ的面积时,QE的长是多少厘米?
当QE恰好平分△APQ的面积时,QE的长是多少厘米?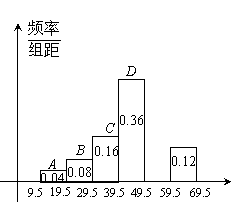 为了解各年龄段观众对某电视剧的收视率,某校初三(1)班的一个研究性学习小组,调查了部分观众的收视情况并分成A、B、C、D、E、F六组进行整理,其频率分布直方图如图所示,请回答:
为了解各年龄段观众对某电视剧的收视率,某校初三(1)班的一个研究性学习小组,调查了部分观众的收视情况并分成A、B、C、D、E、F六组进行整理,其频率分布直方图如图所示,请回答:
 求证:EF=DG
求证:EF=DG