25、
⑴解:方法一:
∵B点坐标为(0.2),
∴OB=2,
∵矩形CDEF面积为8,
∴CF=4.
|
设抛物线的解析式为 .
.
其过三点A(0,1),C(-2.2),F(2,2)。
|

解这个方程组,得
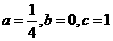
∴此抛物线的解析式为 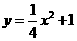 ………… (4分)
………… (4分)
方法二:
∵B点坐标为(0.2),
∴OB=2,
∵矩形CDEF面积为8,
∴CF=4.
∴C点坐标为(一2,2)。 ……… (1分)
根据题意可设抛物线解析式为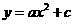 。
。
其过点A(0,1)和C(-2.2)
|

解这个方程组,得
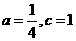
|
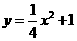
(2)解:

①过点B作BN ,垂足为N.
,垂足为N.
∵P点在抛物线y=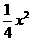 十l上.可设P点坐标为
十l上.可设P点坐标为 .
.
∴PS= ,OB=NS=2,BN=
,OB=NS=2,BN= 。
。
∴PN=PS-NS= ………………………… (6分)
………………………… (6分)
在Rt PNB中.
PNB中.
PB=
∴PB=PS= ………………………… (7分)
………………………… (7分)
②根据①同理可知BQ=QR。
∴ ,
,
又∵  ,
,
∴ ,
,
同理 SBP=
SBP= ………………………… (8分)
………………………… (8分)
∴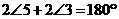
∴
∴ .
.
∴ △SBR为直角三角形.………………………… (9分)
③方法一:
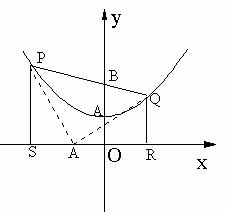 设
设 ,
,
∵由①知PS=PB=b.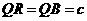 ,
, 。
。
∴
|
 。………………………… (10分)
。………………………… (10分)
假设存在点M.且MS= ,别MR=
,别MR= 。
。
若使△PSM∽△MRQ,
则有 。
。
即 …………… (12分)
…………… (12分)
∴ 。
。
∴SR=2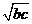
∴M为SR的中点.
∴当点M为SR的中点时. PSM∽
PSM∽ MRQ………………………… (14分)
MRQ………………………… (14分)
方法二:
∵ PSM∽
PSM∽ MRQ
MRQ  ,
,
∴ SPM=
SPM= RMQ,
RMQ, SMP=
SMP= RQM.
RQM.
由直角三角形两锐角互余性质.知 PMS+
PMS+ QMR=
QMR= 。
。
∴ 。………………………… (10分)
。………………………… (10分)
取PQ中点为N.连结MN.则MN= PQ=
PQ= .…………………… (12分)
.…………………… (12分)
∴MN为直角梯形SRQP的中位线,
∴点M为SR的中点 …………………… (14分)
|
|
20、解:
|
|
平均数 |
中位数 |
体能测试成 绩合格次数 |
|
甲 |
60 |
65 |
2 |
|
乙 |
60 |
57.5 |
4 |
(1)
|
………4分
⑵①依据平均数与成绩合格的次数比较甲和乙, 乙 的体能测试成绩较好;………5分
②依据平均数与中位数比较甲和乙, 甲 的体能测试成绩较好。 ………6分
⑶从折线统计图发展趋势来看,乙运动员体能训练的效果较好。 ………10分
(答案不唯一,只要有理有据就给分)
 B.
B.  C.
C.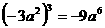 D.
D.

 …1分
…1分
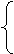
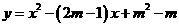
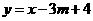 ………7分
………7分 ………8分
………8分 ………10分
………10分 ………12分
………12分
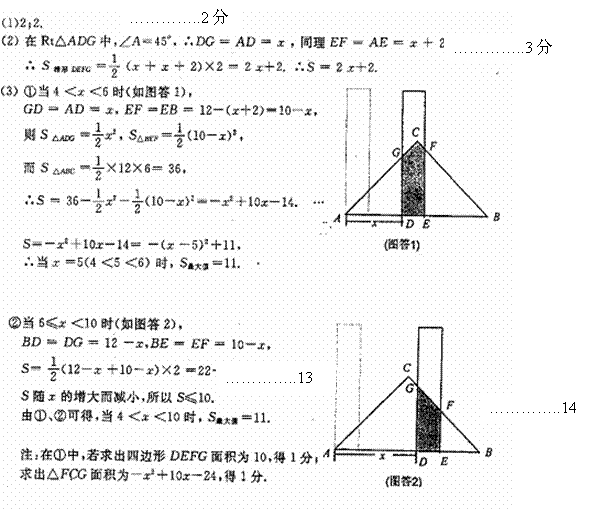
 ………2分
………2分
 4.5 (AB>0)………5分
4.5 (AB>0)………5分 ………8分
………8分 26.6°<45°
………11分
26.6°<45°
………11分