0 137347 137355 137361 137365 137371 137373 137377 137383 137385 137391 137397 137401 137403 137407 137413 137415 137421 137425 137427 137431 137433 137437 137439 137441 137442 137443 137445 137446 137447 137449 137451 137455 137457 137461 137463 137467 137473 137475 137481 137485 137487 137491 137497 137503 137505 137511 137515 137517 137523 137527 137533 137541 447348

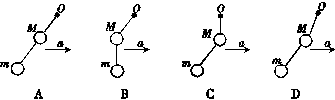
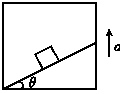 如图甲所示,一物体放置在倾角为θ的斜面上,斜面固定于加速上升的电梯中,加速度为a.在物体始终相对斜面静止的情况下,下列说法正确的是( )
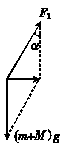
如图甲所示,一物体放置在倾角为θ的斜面上,斜面固定于加速上升的电梯中,加速度为a.在物体始终相对斜面静止的情况下,下列说法正确的是( )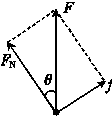 解法一 物体随电梯加速上升,斜面对物体的作用力F=m(g+a)
解法一 物体随电梯加速上升,斜面对物体的作用力F=m(g+a)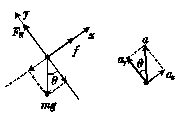
 如图所示,光滑水平地面上的小车的质量为M,站在小车水平底板上的人的质量为m,且m≠M.人用一根跨过定滑轮的绳子拉小车,定滑轮上下两侧的绳子都保持水平,不计绳与滑轮之间的摩擦.关于人和车一起向右加速运动的过程,下列说法正确的是( )
如图所示,光滑水平地面上的小车的质量为M,站在小车水平底板上的人的质量为m,且m≠M.人用一根跨过定滑轮的绳子拉小车,定滑轮上下两侧的绳子都保持水平,不计绳与滑轮之间的摩擦.关于人和车一起向右加速运动的过程,下列说法正确的是( )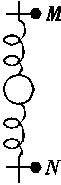
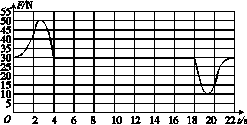
 A.小球将开始做自由落体运动
A.小球将开始做自由落体运动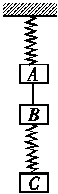 a==g.
a==g.