摘要：已知椭圆的中心在坐标原点.焦点在坐标轴上.且经过..三点． (1)求椭圆的方程: (2)若点D为椭圆上不同于.的任意一点..当内切圆的面积最大时.求内切圆圆心的坐标, (3)若直线与椭圆交于.两点.证明直线与直线的交点在直线上．
网址：http://m.1010jiajiao.com/timu3_id_528645[举报]
已知椭圆的中心在坐标原点，焦点在x轴上，以其两个焦点和短轴的两个端点为顶点的四边形是一个面积为4的正方形，设P为该椭圆上的动点，C、D的坐标分别是（-
，0），（
，0），则PC•PD的最大值为（ ）
| 2 |
| 2 |
| A、4 | ||
B、2
| ||
| C、3 | ||
D、2
|
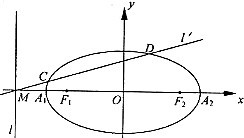已知椭圆的中心在坐标原点，焦点F1、F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，| MA1 |
| A1F1 |
（I）求椭圆的标准方程；
（Ⅱ）过点M的直线l'与椭圆交于C、D两点，若
| OC |
| OD |