摘要:2. 设A.B是椭圆上的两点.点N(1.3)是线段AB的中点.线段AB的垂直平分线与椭圆相交于C.D两点. (Ⅰ)确定的取值范围.并求直线AB的方程, (Ⅱ)试判断是否存在这样的.使得A.B.C.D四点在同一个圆上?并说明理由. (此题不要求在答题卡上画图) 本小题主要考查直线.圆和椭圆等平面解析几何的基础知识以及推理运算能力和综合解决问题的能力. (Ⅰ)解法1:依题意.可设直线AB的方程为.整理得 ① 设是方程①的两个不同的根. ∴ ② 且由N(1.3)是线段AB的中点.得 解得k=-1.代入②得.的取值范围是. 于是.直线AB的方程为 解法2:设则有 依题意. ∵N(1.3)是AB的中点. ∴ 又由N(1.3)在椭圆内.∴ ∴的取值范围是. 直线AB的方程为y-3=-(x-1).即x+y-4=0. (Ⅱ)解法1:∵CD垂直平分AB.∴直线CD的方程为y-3=x-1.即x-y+2=0. 代入椭圆方程.整理得 又设CD的中点为是方程③的两根. ∴ 于是由弦长公式可得 ④ 将直线AB的方程x+y-4=0.代入椭圆方程得 ⑤ 同理可得 ⑥ ∵当时. 假设存在>12.使得A.B.C.D四点共圆.则CD必为圆的直径.点M为圆心. 点M到直线AB的距离为 ⑦ 于是.由④.⑥.⑦式和勾股定理可得 故当>12时.A.B.C.D四点匀在以M为圆心.为半径的圆上. (注:上述解法中最后一步可按如下解法获得:) A.B.C.D共圆△ACD为直角三角形.A为直角|AN|2=|CN|·|DN|. 即 ⑧ 由⑥式知.⑧式左边 由④和⑦知.⑧式右边 ∴⑧式成立.即A.B.C.D四点共圆. 解法2:由(Ⅱ)解法1及λ>12, ∵CD垂直平分AB. ∴直线CD方程为.代入椭圆方程.整理得 ③ 将直线AB的方程x+y-4=0.代入椭圆方程.整理得 ⑤ 解③和⑤式可得 不妨设 ∴ 计算可得.∴A在以CD为直径的圆上. 又B为A关于CD的对称点.∴A.B.C.D四点共圆. (注:也可用勾股定理证明AC⊥AD)
网址:http://m.1010jiajiao.com/timu3_id_528230[举报]
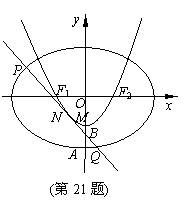 (本小题满分12分) 设椭圆C1:
(本小题满分12分) 设椭圆C1:![]() 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:![]() 与y轴的交点为B,且经过F1,F2点.
与y轴的交点为B,且经过F1,F2点.
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设M(0,![]() ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求![]() 面积的最大值.
面积的最大值.
本小题满分12分)
如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N在x轴上,椭圆C2的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点按纵坐标从大到小依次为A,B,C,D.
(I)设 ,求
,求 与
与 的比值;
的比值;
(II)当e变化时,是否存在直线l,使得BO∥AN,并说明理由
(本小题满分12分)椭圆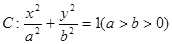 的两个焦点分别为
的两个焦点分别为 ,
,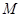 是椭圆短轴的一个端点,且满足
是椭圆短轴的一个端点,且满足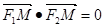 ,点N( 0 , 3 )到椭圆上的点的最远距离为
,点N( 0 , 3 )到椭圆上的点的最远距离为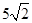
(1)求椭圆C的方程
(2)设斜率为k(k¹0)的直线l与椭圆C相交于不同的两点A、B,Q为AB的中点,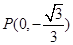 ;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由。
;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由。
查看习题详情和答案>>
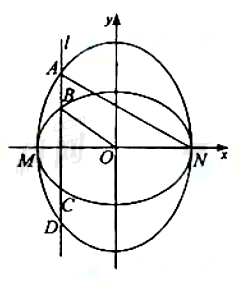
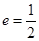 ,求
,求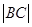 与
与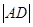 的比值;
的比值;