题目内容
本小题满分12分)
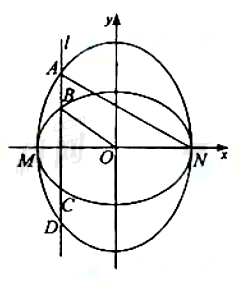
如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N在x轴上,椭圆C2的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点按纵坐标从大到小依次为A,B,C,D.
(1)设
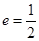 ,求
,求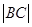 与
与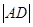 的比值;
的比值;(2)当e变化时,是否存在直线l,使得BO∥AN,并说明理由
(1)
(2)当 时,不存在直线l,使得BO//AN;当
时,不存在直线l,使得BO//AN;当 时,存在直线l使得BO//AN
时,存在直线l使得BO//AN
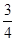
(2)当
 时,不存在直线l,使得BO//AN;当
时,不存在直线l,使得BO//AN;当 时,存在直线l使得BO//AN
时,存在直线l使得BO//AN(1)因为C1,C2的离心率相同,故依题意可设
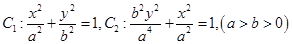 .
.
设直线 分别和C1,C2联立,求得
分别和C1,C2联立,求得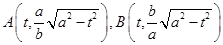 .
.
当 时,
时, ,分别用yA,yB表示A、B的纵坐标,可知
,分别用yA,yB表示A、B的纵坐标,可知
|BC|:AD|=
(2)t=0时的l不符合题意,t≠0时,BO//AN当且仅当BO的斜率kBO与AN的斜率kAN相等,即
 ,
,
解得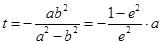 .
.
因为 ,又
,又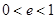 ,所以
,所以 ,解得
,解得 .
.
所以当 时,不存在直线l,使得BO//AN;当
时,不存在直线l,使得BO//AN;当 时,存在直线l使得BO//AN.
时,存在直线l使得BO//AN.
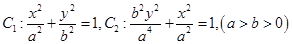 .
.设直线
 分别和C1,C2联立,求得
分别和C1,C2联立,求得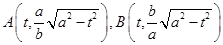 .
.当
 时,
时, ,分别用yA,yB表示A、B的纵坐标,可知
,分别用yA,yB表示A、B的纵坐标,可知|BC|:AD|=

(2)t=0时的l不符合题意,t≠0时,BO//AN当且仅当BO的斜率kBO与AN的斜率kAN相等,即
 ,
,解得
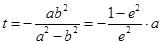 .
.因为
 ,又
,又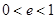 ,所以
,所以 ,解得
,解得 .
.所以当
 时,不存在直线l,使得BO//AN;当
时,不存在直线l,使得BO//AN;当 时,存在直线l使得BO//AN.
时,存在直线l使得BO//AN.
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
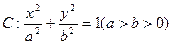 的离心率为
的离心率为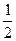 ,且经过点
,且经过点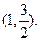
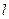 过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率
过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率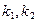 满足
满足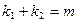 (定值
(定值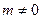 ),求直线
),求直线 是椭圆
是椭圆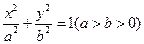 的左、右焦点,过点
的左、右焦点,过点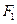 作
作 的直线
的直线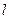 交椭圆于
交椭圆于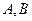 两点,
两点,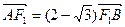 .
.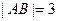 ,求椭圆的标准方程.
,求椭圆的标准方程.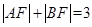 ,则线
,则线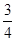
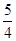
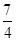
 的焦点在
的焦点在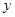 轴上,
轴上, ,
, ,则这样的椭圆个数共有 ( )
,则这样的椭圆个数共有 ( )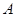 、
、
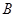 、
、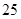
 、
、
 、
、
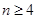 ,
,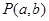 是平面直角坐标系
是平面直角坐标系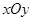 中的点,其中
中的点,其中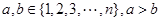
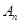 为满足
为满足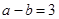 的点
的点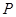 的个数,求
的个数,求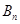 为满足
为满足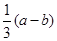 是整数的点
是整数的点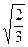 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段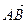 的比为2.
的比为2.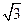 c,0)三点,其中c>0
c,0)三点,其中c>0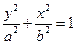
 (其中
(其中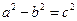 )的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。
)的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。