Question

(本小题满分12分)椭圆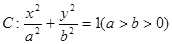的两个焦点分别为 ,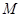是椭圆短轴的一个端点，且满足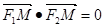，点N( 0 , 3 )到椭圆上的点的最远距离为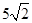

（1）求椭圆C的方程

（2）设斜率为k(k¹0)的直线l与椭圆C相交于不同的两点A、B，Q为AB的中点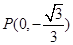，；问A、B两点能否关于过点P、Q的直线对称？若能，求出k的取值范围；若不能，请说明理由。

 

Answer 1

【答案】

（1）

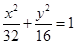
（2）当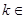( - 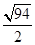, 0 ) ∪( 0 , 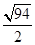)时，A、B两点关于过点P、Q、的直线对称

【解析】

试题分析：解：(1)、椭圆方程可表示为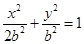……………1分

设H( x , y )是椭圆上的一点，

则| NH |² =x²+(y-3)² =" -" (y+3)²+2b²+18 ，其中 - b≤y≤b

若0＜b＜3 ，则当y =" -" b时，| NH |²有最大值b²+6b+9 ，

所以由b²+6b+9=50解得b = -3±5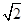 (均舍去) …………………3分

若b≥3，则当y = -3时，| NH |²有最大值2b²+18 ，

所以由2b²+18=50解得b²=16

∴所求椭圆方程为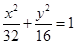………………6分

(ii) 设 A( x₁ , y₁ ) ，B( x₂ , y₂ )，Q( x₀ , y₀ )，

则由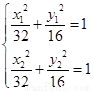两式相减得x₀+2ky₀=0；………①　　……………………8分

又直线PQ⊥直线l，∴直线PQ的方程为y=" -" x - ，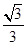

将点Q( x₀ , y₀ )坐标代入得y₀=" -" x₀- 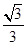………②　　……………………9分

由①②解得Q( ,  )，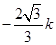

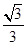而点Q必在椭圆的内部

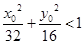∴ ，…………… 10分

由此得k² < ，又k≠0

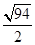∴ - < k < 0或0 < k <

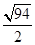
故当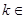( - 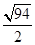, 0 ) ∪( 0 , 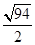)时，A、B两点关于过点P、Q、的直线对称。……12分

考点：本试题考查椭圆方程，直线与椭圆的位置关系。

点评：解决该试题关键的一步是理解到短轴端点的最远的距离的表示，以及能理解和联立方程组，运用点差法得到直线的方程，根据点Q在椭圆内得到参数k的范围，属于中档题。