摘要：有点难度哟! 已知A={x|1＜|x-2|＜2}.B={x|x2-(a+1)x+a＜0}.且A∩B≠.试确定a的取值范围. 解:A={x|0＜x＜1或3＜x＜4}. (1)当a＞1时.B={x|1＜x＜a}. 由A∩B≠.得a＞3. (2)当a＜1时.B={x|a＜x＜1}. 由A∩B≠.易知a＜1. 综上.a的取值范围是{a|a＜1或a＞3}.
网址：http://m.1010jiajiao.com/timu3_id_500613[举报]
△ABC中，角A、B、C的对边依次为a、b、c．已知a=3，b=4，外接圆半径R=
，c边长为整数，
（1）求∠A的大小（用反三角函数表示）；
（2）求边长c；
（3）在AB、AC上分别有点D、E，线段DE将△ABC分成面积相等的两部分，求线段DE长的最小值． 查看习题详情和答案>>
| 5 | 2 |
（1）求∠A的大小（用反三角函数表示）；
（2）求边长c；
（3）在AB、AC上分别有点D、E，线段DE将△ABC分成面积相等的两部分，求线段DE长的最小值． 查看习题详情和答案>>
已知a，b为常数，a?0，函数
．
（1）若a=2，b=1，求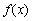
在（0，∞）内的极值；
（2）①若a>0，b>0，求证：
在区间[1，2]上是增函数；
②若
，
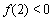，且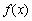
在区间[1，2]上是增函数，求由所有点
形成的平面区域的面积．
查看习题详情和答案>>
已知a，b为常数，a¹0，函数
．
（1）若a=2，b=1，求
在（0，+∞）内的极值；
（2）①若a>0，b>0，求证：在区间[1，2]上是增函数；
②若
，
，且在区间[1，2]上是增函数，求由所有点
形成的平面区域的面积．
．
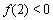
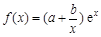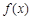在（0，+∞）内的极值；
，
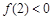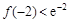，且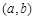
形成的平面区域的面积．