题目内容
已知a,b为常数,a?0,函数 .
.
(1)若a=2,b=1,求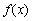 在(0,∞)内的极值;
在(0,∞)内的极值;
(2)①若a>0,b>0,求证: 在区间[1,2]上是增函数;
在区间[1,2]上是增函数;
②若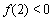 ,
, ,且
,且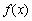 在区间[1,2]上是增函数,求由所有点
在区间[1,2]上是增函数,求由所有点 形成的平面区域的面积.
形成的平面区域的面积.
【答案】
(1) ,(2)①详见解析,②
,(2)①详见解析,②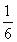
【解析】
试题分析:(1)求具体函数极值问题分三步,一是求导,二是求根,三是列表,关键在于正确求出导数,即 ;求根时需结合定义区间进行取舍,如根据定义区间
;求根时需结合定义区间进行取舍,如根据定义区间 舍去负根;列表时需注意导数在对应区间的符号变化规律,这样才可得出正确结论,因为导数为零的点不一定为极值点,极值点附近导数值必须要变号,(2)①利用导数证明函数单调性,首先要正确转化,如本题只需证到在区间[1,2]上
舍去负根;列表时需注意导数在对应区间的符号变化规律,这样才可得出正确结论,因为导数为零的点不一定为极值点,极值点附近导数值必须要变号,(2)①利用导数证明函数单调性,首先要正确转化,如本题只需证到在区间[1,2]上 成立即可,由
成立即可,由 得只需证到在区间[1,2]上
得只需证到在区间[1,2]上 ,因为对称轴
,因为对称轴
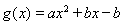 在区间[1,2]上单调增,因此只需证
在区间[1,2]上单调增,因此只需证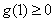 ,而这显然成立,②中条件“
,而这显然成立,②中条件“ 在区间[1,2]上是增函数”与①不同,它是要求
在区间[1,2]上是增函数”与①不同,它是要求 在区间[1,2]上恒成立,结合二次函数图像可得关于
在区间[1,2]上恒成立,结合二次函数图像可得关于 不等关系,再考虑
不等关系,再考虑 ,
, ,可得可行域.
,可得可行域.
试题解析:(1)解: 2分
2分
当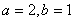 时,
时,  ,
,
令 得
得 或
或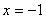 (舍去) 4分
(舍去) 4分
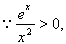 当
当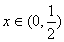 时,
时, 
 是减函数,
是减函数,
当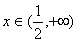 时,
时,
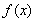 是增函数
是增函数
所以当 时,
时,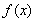 取得极小值为
取得极小值为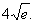 6分
6分
(2)令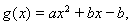
①证明: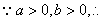 二次函数
二次函数 的图象开口向上,
的图象开口向上,
对称轴 且
且 8分
8分
 对一切
对一切 恒成立.
恒成立.
又
 对一切
对一切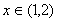 恒成立.
恒成立.
 函数图象是不间断的,
函数图象是不间断的,
 在区间
在区间 上是增函数. 10分
上是增函数. 10分
②解: 
 即
即
 在区间
在区间 上是增函数
上是增函数
 对
对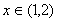 恒成立.
恒成立.
则 对
对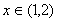 恒成立.
恒成立.
 12分
12分
在(*)(**)的条件下, 且
且
且 恒成立.
恒成立.
综上,点 满足的线性约束条件是
满足的线性约束条件是 14分
14分
由所有点 形成的平面区域为
形成的平面区域为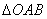 (如图所示),
(如图所示),
其中
则
即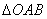 的面积为
的面积为 . 16分
. 16分
考点:求函数极值,二次函数恒成立,线性规划求面积.

练习册系列答案
相关题目