网址:http://m.1010jiajiao.com/timu3_id_500047[举报]
如图,边长为2的正方形ABCD,E是BC的中点,沿AE,DE将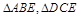 折起,使得B与C重合于O.
折起,使得B与C重合于O.
(Ⅰ)设Q为AE的中点,证明:QD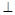 AO;
AO;
(Ⅱ)求二面角O—AE—D的余弦值.
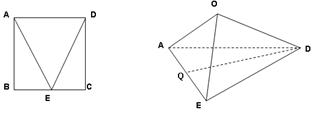
【解析】第一问中,利用线线垂直,得到线面垂直,然后利用性质定理得到线线垂直。取AO中点M,连接MQ,DM,由题意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因为Q为AE的中点,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
第二问中,作MN AE,垂足为N,连接DN
AE,垂足为N,连接DN
因为AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因为AO DM ,DM
DM ,DM 平面AOE
平面AOE
因为MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=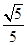 ,DN=
,DN= ,COS
,COS DNM=
DNM=
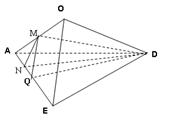
(1)取AO中点M,连接MQ,DM,由题意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因为Q为AE的中点,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
(2)作MN AE,垂足为N,连接DN
AE,垂足为N,连接DN
因为AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因为AO DM ,DM
DM ,DM 平面AOE
平面AOE
因为MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=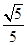 ,DN=
,DN= ,COS
,COS DNM=
DNM=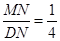
二面角O-AE-D的平面角的余弦值为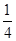
查看习题详情和答案>>
设数列 的各项均为正数.若对任意的
的各项均为正数.若对任意的 ,存在
,存在 ,使得
,使得 成立,则称数列
成立,则称数列 为“Jk型”数列.
为“Jk型”数列.
(1)若数列 是“J2型”数列,且
是“J2型”数列,且 ,
, ,求
,求 ;
;
(2)若数列 既是“J3型”数列,又是“J4型”数列,证明:数列
既是“J3型”数列,又是“J4型”数列,证明:数列 是等比数列.
是等比数列.
【解析】1)中由题意,得 ,
, ,
, ,
, ,…成等比数列,且公比
,…成等比数列,且公比 ,
,
所以.
(2)中证明:由{ }是“j4型”数列,得
}是“j4型”数列,得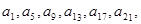 ,…成等比数列,设公比为t. 由{
,…成等比数列,设公比为t. 由{ }是“j3型”数列,得
}是“j3型”数列,得
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 …成等比数列,设公比为
…成等比数列,设公比为 ;
;
查看习题详情和答案>>
[番茄花园1] (本题满分)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足 。
。
(Ⅰ)求角C的大小;
(Ⅱ)求 的最大值。
的最大值。
(Ⅰ)解:由题意可知
 absinC=
absinC= ,2abcosC.
,2abcosC.
所以tanC= .
.
因为0<C< ,
,
所以C= .
.
(Ⅱ)解:由已知sinA+sinB=sinA+sin( -C-A)=sinA+sin(
-C-A)=sinA+sin( -A)
-A)
=sinA+ cosA+
cosA+ sinA=
sinA= sin(A+
sin(A+ )≤
)≤ .
.
当△ABC为正三角形时取等号,
所以sinA+sinB的最大值是 .
.
[番茄花园1]1.
查看习题详情和答案>>如图,已知圆锥体 的侧面积为
的侧面积为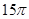 ,底面半径
,底面半径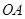 和
和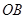 互相垂直,且
互相垂直,且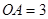 ,
, 是母线
是母线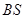 的中点.
的中点.

(1)求圆锥体的体积;
(2)异面直线 与
与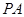 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
【解析】本试题主要考查了圆锥的体积和异面直线的所成的角的大小的求解。
第一问中,由题意, 得
得 ,故
,故
从而体积 .2中取OB中点H,联结PH,AH.
.2中取OB中点H,联结PH,AH.
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
解:(1)由题意, 得
得 ,
,
故 从而体积
从而体积 .
.
(2)如图2,取OB中点H,联结PH,AH.
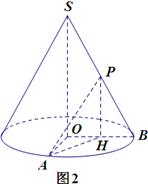
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
查看习题详情和答案>>
 (
( 为实数).
为实数). 时,求
时,求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 . ∵
. ∵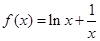 ∴
∴
 .
. 时,
时, ;
当
;
当 时,
时, . 故
. 故 .
.
 时,
时, ,在
,在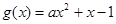 ,则
,则
 或
或 在
在 ,且
,且
 或
或
 或
或
 或
或
 或
或 . 综上
. 综上