摘要:20.如图.在矩形ABCD中.AB=12cm.BC=8cm.点E.F.G分别从点A.B.C三点同时出发.沿矩形的边按逆时针方向移动.点E.G的速度均为2cm/s.点F的速度为4cm/s.当点F追上点G(即点F与点G重合)时.三个点随之停止移动.设移动开始后第t秒时.△EFG的面积为S(cm2). (1)当t=1秒时.S的值是多少? (2)写出S和t之间的函数解析式.并指出自变量t的取值范围. (3)若点F在矩形的边BC上移动.当t为何值时.以点E.B.F为顶点的三角形与以F.C.G为顶点的三角形相似?请说明理由. [答案](1)如图甲.当t=1秒时.AE=2.EB=10.BF=4.FC=4.CG=2.由S=S梯形EGCG-SEBF-SFCG=×8-×10×4-×4×2=24 .当0≤t≤2时.点E.F.G分别在AB.BC.CD上移动.此时AE=2t.EB=12-2t.BF=4t.FC=8-4t.S=8t2-32t+48 (3)如图乙.当点F追上点G时.4t=2t=8.解得t=4.当2<t≤4时.CF=4t-8.CG=2t.FG=CG-CF=8-2t.即S=-8t+32. .当点F在矩形的边BC上移动时.0≤t≤2.在EFF和FCG中.B=C=90..①若.即.解得t=.又t=满足0≤t≤2.所以当t=时△EBF∽△GCF②若.即.解得t=.又t=满足0≤t≤2.所以当t=时△EBF∽△GCF.综上知.当t=或时.以点E.B.F为顶点的三角形与以F.C.G为顶点的三角形相似
网址:http://m.1010jiajiao.com/timu3_id_496554[举报]
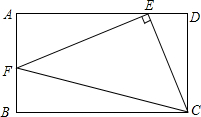 如图,在矩形ABCD中,已知AB=2,BC=3,点E为AD边上一动点(不与A、D重合),连接CE,作EF⊥CE交AB边于F
如图,在矩形ABCD中,已知AB=2,BC=3,点E为AD边上一动点(不与A、D重合),连接CE,作EF⊥CE交AB边于F(1)求证:△AEF∽△DCE;
(2)当△ECF∽△AEF时,求AF的长.
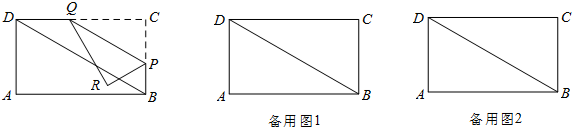
(2012•滨海县二模)如图,在矩形ABCD中,AB=9,AD=3
,点P是边BC上的动点(点P不与点B、点C重合),过点P作直线PQ∥BD,交CD边于Q点,再把△PQC沿着动直线PQ对折,点C的对应点是R点,设CP的长度为x,△PQR与矩形ABCD重叠部分的面积为y.
(1)求∠CQP的度数;
(2)当x取何值时,点R落在矩形ABCD的边AB上?
(3)求y与x之间的函数关系式.
查看习题详情和答案>>
| 3 |
(1)求∠CQP的度数;
(2)当x取何值时,点R落在矩形ABCD的边AB上?
(3)求y与x之间的函数关系式.

如图,在矩形ABCD中,AB=24,BC=26.先顺次连接矩形各边中点得菱形,又顺次连接菱形各边中点得矩形,再顺次连接矩形各边中点得菱形,照此继续,…,第10次连接的图形的面积是 .
 查看习题详情和答案>>
查看习题详情和答案>>
 查看习题详情和答案>>
查看习题详情和答案>>
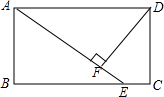 垂足为F.设AE=xcm,DF=ycm.
垂足为F.设AE=xcm,DF=ycm.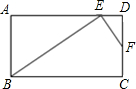 如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE△∽△DEF,AB=6,AE=8,DE=2,求EF的长.
如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE△∽△DEF,AB=6,AE=8,DE=2,求EF的长.