摘要：13．(2010年广州中考数学模拟试题(四))如图.在矩形ABCD中.AE平分∠DAB交DC于点E.连接BE.过E作EF⊥BE交AD于E. (1)∠DEF和∠CBE相等吗?请说明理由: (2)请找出图中与EB相等的线段.并说明理由. 答案:(1)相等. ∵四边形ABCD是矩形, ∴∠C=∠D=90°. ∴∠BEC+∠CBE=90°. ∵EF⊥BE, ∴∠BEF=90°. ∴∠DEF+∠BEC=90°. ∴∠DEF=∠CBE. (2)BE=EF. ∵AE平分∠DAB, ∴∠DAE=∠BAE. ∵AB∥CD, ∴∠BAE=∠DEA. ∴∠DAE=∠DEA . ∴AD=ED=BCA. ∵∠C=∠D=90°, ∠DEF=∠CBE, ∴△DEF≌△CBE(ASA). ∴BE=EF.
网址：http://m.1010jiajiao.com/timu3_id_488683[举报]
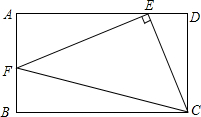如图，在矩形ABCD中，已知AB=2，BC=3，点E为AD边上一动点（不与A、D重合），连接CE，作EF⊥CE交AB边于F（1）求证：△AEF∽△DCE；
（2）当△ECF∽△AEF时，求AF的长．
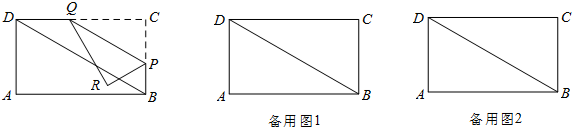
（2012•滨海县二模）如图，在矩形ABCD中，AB=9，AD=3
，点P是边BC上的动点（点P不与点B、点C重合），过点P作直线PQ∥BD，交CD边于Q点，再把△PQC沿着动直线PQ对折，点C的对应点是R点，设CP的长度为x，△PQR与矩形ABCD重叠部分的面积为y．
（1）求∠CQP的度数；
（2）当x取何值时，点R落在矩形ABCD的边AB上？
（3）求y与x之间的函数关系式．
查看习题详情和答案>>
| 3 |
（1）求∠CQP的度数；
（2）当x取何值时，点R落在矩形ABCD的边AB上？
（3）求y与x之间的函数关系式．
如图，在矩形ABCD中，AB=24，BC=26．先顺次连接矩形各边中点得菱形，又顺次连接菱形各边中点得矩形，再顺次连接矩形各边中点得菱形，照此继续，…，第10次连接的图形的面积是 ．
查看习题详情和答案>>
查看习题详情和答案>>
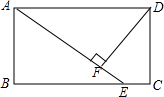垂足为F．设AE=xcm，DF=ycm．
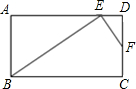如图，在矩形ABCD中，点E、F分别在边AD、DC上，△ABE△∽△DEF，AB=6，AE=8，DE=2，求EF的长．