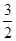摘要:12.抛物线y=ax2+(b-1)x+2. ., 求此抛物线的解析式; (2) 若此抛物线与直线y=x有两个不同的交点P.Q,且点P.Q关于原点对称. ① 求b的值; ② 请在横线上填上一个符合条件的a的值: a = ,并在此条件下画出该函数的图象. (15)二次函数 考试内容] 二次函数及其图象.一元二次方程的近似解. [考试要求] ①通过对实际问题情境的分析确定二次函数的表达式.并体会二次函数的意义. ②会用描点法画出二次函数的图象.能从图象上认识二次函数的性质. ③会根据公式确定图象的顶点.开口方向和对称轴.并能解决简单的实际问题. ④会利用二次函数的图象求一元二次方程的近似解. [考点复习]
网址:http://m.1010jiajiao.com/timu3_id_453627[举报]
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.

(1)求抛物线的解析式.
(2)已知AD=AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t秒的移动,线段PQ被BD垂直平分,求t的值;
(3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC的值最小?若存在,请求出点M的坐标;若不存在,请说明理由.
(注:抛物线y=ax2+bx+c的对称轴为![]() )
)
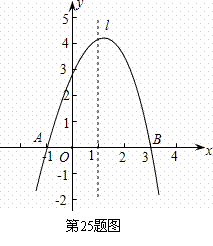
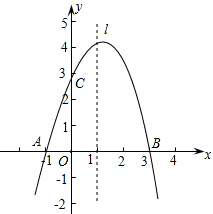
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
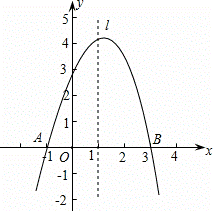
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
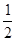 x2+x+
x2+x+