题目内容
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.

(1)求抛物线的解析式.
(2)已知AD=AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t秒的移动,线段PQ被BD垂直平分,求t的值;
(3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC的值最小?若存在,请求出点M的坐标;若不存在,请说明理由.
(注:抛物线y=ax2+bx+c的对称轴为![]() )
)
解析:
|
(1)解法一:设抛物线的解析式为y=a(x+3)(x-4) 因为B(0,4)在抛物线上,所以4=a(0+3)(0-4)解得a=-1/3 解法二:设抛物线的解析式为 依题意得:c=4且 所以 所求的抛物线的解析式为
(2)连接DQ,在Rt△AOB中, 所以AD=AB=5,AC=AD+CD=3+4=7,CD=AC-AD=7-5=2 因为BD垂直平分PQ,所以PD=QD,PQ⊥BD,所以∠PDB=∠QDB 因为AD=AB,所以∠ABD=∠ADB,∠ABD=∠QDB,所以DQ∥AB 所以∠CQD=∠CBA.∠CDQ=∠CAB,所以△CDQ∽△CAB 所以AP=AD-DP=AD-DQ=5- 所以t的值是 (3)答对称轴上存在一点M,使MQ+MC的值最小 理由:因为抛物线的对称轴为 所以A(-3,0),C(4,0)两点关于直线 连接AQ交直线 过点Q作QE⊥x轴,于E,所以∠QED=∠BOA=900 DQ∥AB,∠BAO=∠QDE,△DQE∽△ABO 所以QE= 设直线AQ的解析式为 则 所以直线AQ的解析式为 则:在对称轴上存在点M |

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案


 由此得
由此得


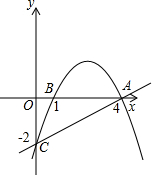 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点. 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点,
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点, (2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,
(2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG, (2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).
(2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).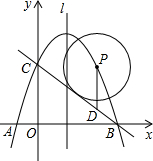 如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).
如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).