Question

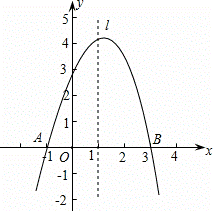
已知抛物线y＝ax²＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．

(1)求抛物线的函数关系式；

(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；

(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．

Answer 1

考点：

二次函数综合题。

专题：

综合题；分类讨论。

分析：

(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可．

(2)由图知：A、B点关于抛物线的对称轴对称，那么根据抛物线的对称性以及两点之间线段最短可知：若连接BC，那么BC与直线l的交点即为符合条件的P点．

(3)由于△MAC的腰和底没有明确，因此要分三种情况来讨论：①MA＝AC、②MA＝MC、②AC＝MC；可先设出M点的坐标，然后用M点纵坐标表示△MAC的三边长，再按上面的三种情况列式求解．

解答：

解：(1)将A(－1，0)、B(3，0)、C(0，3)代入抛物线y＝ax²＋bx＋c中，得：

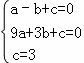，解得：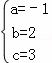

∴抛物线的解析式：y＝－x²＋2x＋3．

(2)连接BC，直线BC与直线l的交点为P；

设直线BC的解析式为y＝kx＋b，将B(3，0)，C(0，3)代入上式，得：

，解得：

∴直线BC的函数关系式y＝－x＋3；

当x－1时，y＝2，即P的坐标(1，2)．

(3)抛物线的解析式为：x＝－＝1，设M(1，m)，已知A(－1，0)、C(0，3)，则：

MA²＝m²＋4，MC²＝m²－6m＋10，AC²＝10；

①若MA＝MC，则MA²＝MC²，得：

m²＋4＝m²－6m＋10，得：m＝1；

②若MA＝AC，则MA²＝AC²，得：

m²＋4＝10，得：m＝±；

③若MC＝AC，则MC²＝AC²，得：

m²－6m＋10＝10，得：m＝0，m＝6；

当m＝6时，M、A、C三点共线，构不成三角形，不合题意，故舍去；

综上可知，符合条件的M点，且坐标为 M(1，)(1，－)(1，1)(1，0)．

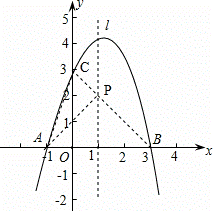
点评：

该二次函数综合题涉及了抛物线的性质及解析式的确定、等腰三角形的判定等知识，在判定等腰三角形时，一定要根据不同的腰和底分类进行讨论，以免漏解．