摘要:22.已知函数:. (1)当的定义域为时.求证:的值域为, (2)设函数.求的最小值 . 解:(1)证明:. 当.... ∴. 即的值域为. ------4分 (2) ①当. 如果 即时.则函数在上单调递增. ∴ , ------6分 如果, 当时.最小值不存在. --------8分 ②当. 如果, --------10分 如果 --------12分 当. . -------13分 综合得:当时. g(x)最小值是,当时. g(x)最小值是 ,当时. g(x)最小值为,当时. g(x)最小值不存在. -------14分
网址:http://m.1010jiajiao.com/timu3_id_4473442[举报]
(本小题共14分)已知 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 .
.
(Ⅰ)判断函数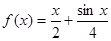 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合 中的元素
中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为
的定义域为 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 有且只有一个实数根;
有且只有一个实数根;
(Ⅲ)对任意 ,且
,且 ,求证:对于
,求证:对于 定义域中任意的
定义域中任意的 ,
, ,
,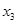 ,当
,当 ,且
,且 时,
时, .
.
查看习题详情和答案>>
(本小题满分14分) 对函数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,
m+mk],k∈Z,m>0,n>0,且m、n为常数)为Φ(x)的第k阶阶梯函数,m叫做阶宽,n叫做阶高,已知阶宽为2,阶高为3.
(1)当Φ(x)=2x时 ①求f0(x)和fk(x)的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
查看习题详情和答案>>
(本小题满分14分) 对函数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,
m+mk],k∈Z,m>0,n>0,且m、n为常数)为Φ(x)的第k阶阶梯函数,m叫做阶宽,n叫做阶高,已知阶宽为2,阶高为3.
(1)当Φ(x)=2x时 ①求f0(x)和fk(x)的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
(2)若Φ(x)=x2,则是否存在正整数k,使得不等式fk(x)<(1-3k)x+4k2+3k-1有解?若存在,求出k的值;若不存在,请说明理由.
查看习题详情和答案>>
 数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,
数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk, )当Φ(x)=2x时 ①求f0(x)和fk
)当Φ(x)=2x时 ①求f0(x)和fk (x)
(x) 的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线; 数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk,
数Φ(x),定义fk(x)=Φ(x-mk)+nk(其中x∈(mk, (x)
(x) 的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;
的解析式; ②求证:Φ(x)的各阶阶梯函数图象的最高点共线;