题目内容
(本小题共14分)已知 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 .
.
(Ⅰ)判断函数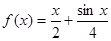 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合 中的元素
中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为
的定义域为 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 有且只有一个实数根;
有且只有一个实数根;
(Ⅲ)对任意 ,且
,且 ,求证:对于
,求证:对于 定义域中任意的
定义域中任意的 ,
, ,
,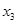 ,当
,当 ,且
,且 时,
时, .
.
【答案】
解:(Ⅰ)因为①当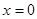 时,
时,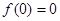 ,
,
所以方程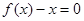 有实数根0;
有实数根0;
②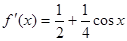 ,
,
所以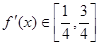 ,满足条件
,满足条件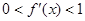 ;
;
由①②,函数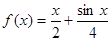 是集合
是集合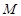 中的元素. …………5分
中的元素. …………5分
(Ⅱ)假设方程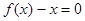 存在两个实数根
存在两个实数根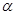 ,
,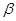
 ,
,
则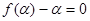 ,
, .
.
不妨设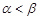 ,根据题意存在
,根据题意存在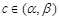 ,
,
满足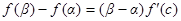 .
.
因为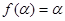 ,
,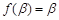 ,且
,且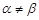 ,所以
,所以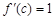 .
.
与已知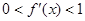 矛盾.又
矛盾.又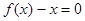 有实数根,
有实数根,
所以方程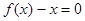 有且只有一个实数根. …………10分
有且只有一个实数根. …………10分
(Ⅲ)当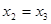 时,结论显然成立;
时,结论显然成立;
当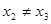 ,不妨设
,不妨设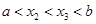 .
.
因为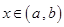 ,且
,且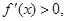 所以
所以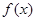 为增函数,那么
为增函数,那么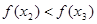 .
.
又因为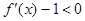 ,所以函数
,所以函数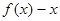 为减函数,
为减函数,
所以 .
.
所以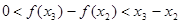 ,即
,即 .
.
因为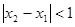 ,所以
,所以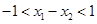 , (1)
, (1)
又因为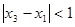 ,所以
,所以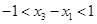 ,
(2)
,
(2)
(1)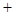 (2)得
(2)得 即
即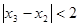 .
.
所以
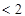 .
.
综上,对于任意符合条件的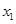 ,
,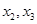 总有
总有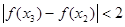 成立.……14分
成立.……14分
【解析】本题是一道以集合为背景的创新题,考查函数的性质和不等式的证明。考查学生的理解能力和分析能力。读懂题意是解题的前提,解题是注意分类讨论思想的应用。

练习册系列答案
相关题目
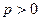 ,动点
,动点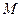 到定点
到定点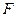
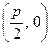 的距离比
的距离比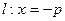 的距离小
的距离小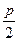 .
.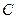 的方程;
的方程; 是轨迹
是轨迹 的两个不同点,
的两个不同点,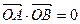 ,求
,求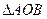 面积的最小值;
面积的最小值;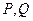 关于直线
关于直线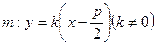 对称?若存在,求出直线
对称?若存在,求出直线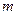 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.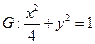 .过点(m,0)作圆
.过点(m,0)作圆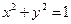 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.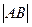 表示为m的函数,并求
表示为m的函数,并求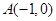 ,
,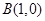 ,动点P满足
,动点P满足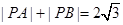 ,记动点P的轨迹为W.
,记动点P的轨迹为W.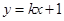 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点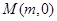 ,使得
,使得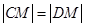 成立,求实数m的取值范围.
成立,求实数m的取值范围.