题目内容
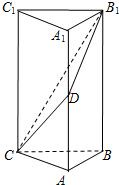 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=1,AA1=2,D是AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=1,AA1=2,D是AA1的中点.(Ⅰ)求异面直线A1C1与B1D所成角的大小;
(Ⅱ)求二面角C-B1D-B的大小;
(Ⅲ)在B1C上是否存在一点E,使得DE∥平面ABC?若存在,求出
| B1E | EC |
分析:(Ⅰ)以B为原点,BC、BA、BB1分别为x、y、z轴,建立空间直角坐标系,求得相关点的坐标,再求得相关向量的坐标,最后利用夹角公式求解.
(Ⅱ)直三棱柱的结构特征,得到B1B⊥BC,再由AB⊥BC,得到BC⊥平面ABB1D.从而有BD⊥B1D,所以BD是CD在平面ABB1D内的射影,∠CDB为二面角C-B1D-B的平面角.
(Ⅲ)由D为中点,则设E为B1C的中点,G为BC的中点,有EG∥BB1,再由EG=
BB1,AD∥BB1,且AD=
BB1,得到四边形ADEG为平行四边形,从而有DE∥AG,从而有DE∥平面ABC结论.
(Ⅱ)直三棱柱的结构特征,得到B1B⊥BC,再由AB⊥BC,得到BC⊥平面ABB1D.从而有BD⊥B1D,所以BD是CD在平面ABB1D内的射影,∠CDB为二面角C-B1D-B的平面角.
(Ⅲ)由D为中点,则设E为B1C的中点,G为BC的中点,有EG∥BB1,再由EG=
| 1 |
| 2 |
| 1 |
| 2 |
解答: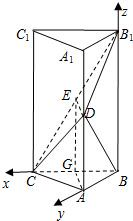 解:(Ⅰ)如图,以B为原点,BC、BA、BB1分别为x、y、z轴,建立空间直角坐标系O-xyz,
解:(Ⅰ)如图,以B为原点,BC、BA、BB1分别为x、y、z轴,建立空间直角坐标系O-xyz,
则B(0,0,0),C(1,0,0),A(0,1,0),
B1(0,0,2),C1(1,0,2),A1(0,1,2),D(0,1,1),
∵
=(1,-1,0),
=(0,1,-1),
∴cos<
,
>=
=-
,
∴异面直线A1C1与B1D所成的角为60°.
(Ⅱ)解:∵直三棱柱ABC-A1B1C1,∴B1B⊥BC,
又AB⊥BC,AB∩BB1=B,∴BC⊥平面ABB1D.
如图,连接BD,
在△BB1D中,∵BD=B1D=
, BB1=2,
∴BD2+B1D2=BB12,即BD⊥B1D,
∵BD是CD在平面ABB1D内的射影,
∴CD⊥B1D,∴∠CDB为二面角C-B1D-B的平面角.
∵
=(1,-1,-1),
=(0,-1,-1),
∴cos∠CDB=
=
,
∴二面角C-B1D-B的大小为arccos
;
(Ⅲ)答:在B1C上存在一点E,使得DE∥平面ABC,此时
=1.
以下给出证明过程.
证明:如图,设E为B1C的中点,G为BC的中点,连接EG,AG,ED,
在△BCB1中,∵BG=GC,B1E=EC,∴EG∥BB1,且EG=
BB1,
又AD∥BB1,且AD=
BB1,
∴EG∥AD,EG=AD,
∴四边形ADEG为平行四边形,∴DE∥AG,
又AG?平面ABC,DE?平面ABC,
∴DE∥平面ABC.
 解:(Ⅰ)如图,以B为原点,BC、BA、BB1分别为x、y、z轴,建立空间直角坐标系O-xyz,
解:(Ⅰ)如图,以B为原点,BC、BA、BB1分别为x、y、z轴,建立空间直角坐标系O-xyz,则B(0,0,0),C(1,0,0),A(0,1,0),
B1(0,0,2),C1(1,0,2),A1(0,1,2),D(0,1,1),
∵
| A1C1 |
| B1D |
∴cos<
| A1C1 |
| B1D |
| ||||
|
|
| 1 |
| 2 |
∴异面直线A1C1与B1D所成的角为60°.
(Ⅱ)解:∵直三棱柱ABC-A1B1C1,∴B1B⊥BC,
又AB⊥BC,AB∩BB1=B,∴BC⊥平面ABB1D.
如图,连接BD,
在△BB1D中,∵BD=B1D=
| 2 |
∴BD2+B1D2=BB12,即BD⊥B1D,
∵BD是CD在平面ABB1D内的射影,
∴CD⊥B1D,∴∠CDB为二面角C-B1D-B的平面角.
∵
| DC |
| DB |
∴cos∠CDB=
| ||||
|
|
| ||
| 3 |
∴二面角C-B1D-B的大小为arccos
| ||
| 3 |
(Ⅲ)答:在B1C上存在一点E,使得DE∥平面ABC,此时
| B1E |
| EC |
以下给出证明过程.
证明:如图,设E为B1C的中点,G为BC的中点,连接EG,AG,ED,
在△BCB1中,∵BG=GC,B1E=EC,∴EG∥BB1,且EG=
| 1 |
| 2 |
又AD∥BB1,且AD=
| 1 |
| 2 |
∴EG∥AD,EG=AD,
∴四边形ADEG为平行四边形,∴DE∥AG,
又AG?平面ABC,DE?平面ABC,
∴DE∥平面ABC.
点评:本题主要考查用向量法求线面角、二面角以及线线、线面与面面平行与垂直关系的转化,综合性较强.

练习册系列答案
相关题目




