题目内容
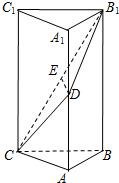 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=1,AA1=2,D、E分别是AA1、B1C的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=1,AA1=2,D、E分别是AA1、B1C的中点.(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求异面直线A1C1与B1D所成角的大小;
(Ⅲ)求二面角C-B1D-B的大小.
分析:(Ⅰ)设G为BC的中点,连接EG,AG,因BG=GC,B1E=EC,则EG∥BB1,且EG=
BB1,又AD∥BB1,且AD=
BB1,则EG∥AD,EG=AD,从而得到四边形ADEG为平行四边形,则DE∥AG,又AG?平面ABC,DE?平面ABC,根据线面平行的判定定理可知DE∥平面ABC.
(Ⅱ)设F为BB1的中点,连接AF,CF,根据直三棱柱ABC-A1B1C1,且D是AA1的中点,则AF∥B1D,A1C1∥AC,从而∠CAF为异面直线A1C1与B1D所成的角或其补角.在Rt△ABF中,求出AF、CF,在△ABC中,求出AC,在△ACF中,即可求出∠CAF;
(Ⅲ)根据直三棱柱ABC-A1B1C1,则B1B⊥BC,又AB⊥BC,AB∩BB1=B,根据线面垂直的判定定理可知BC⊥平面ABB1D,连接BD,在△BB1D中BD2+B1D2=BB12,根据勾股定理可知BD⊥B1D,根据BD是CD在平面ABB1D内的射影,则CD⊥B1D,从而∠CDB为二面角C-B1D-B的平面角,在△BCD中求出此角即可.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)设F为BB1的中点,连接AF,CF,根据直三棱柱ABC-A1B1C1,且D是AA1的中点,则AF∥B1D,A1C1∥AC,从而∠CAF为异面直线A1C1与B1D所成的角或其补角.在Rt△ABF中,求出AF、CF,在△ABC中,求出AC,在△ACF中,即可求出∠CAF;
(Ⅲ)根据直三棱柱ABC-A1B1C1,则B1B⊥BC,又AB⊥BC,AB∩BB1=B,根据线面垂直的判定定理可知BC⊥平面ABB1D,连接BD,在△BB1D中BD2+B1D2=BB12,根据勾股定理可知BD⊥B1D,根据BD是CD在平面ABB1D内的射影,则CD⊥B1D,从而∠CDB为二面角C-B1D-B的平面角,在△BCD中求出此角即可.
解答:(Ⅰ)证明:如图,设G为BC的中点,连接EG,AG,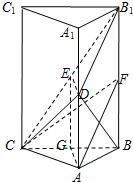
在△BCB1中,∵BG=GC,B1E=EC,∴EG∥BB1,且EG=
BB1,
又AD∥BB1,且AD=
BB1,∴EG∥AD,EG=AD,
∴四边形ADEG为平行四边形,∴DE∥AG,
又AG?平面ABC,DE?平面ABC,∴DE∥平面ABC.
(Ⅱ)解:如图,设F为BB1的中点,连接AF,CF,
∵直三棱柱ABC-A1B1C1,且D是AA1的中点,
∴AF∥B1D,A1C1∥AC,∴∠CAF为异面直线A1C1与B1D所成的角或其补角.
在Rt△ABF中,BF⊥AB,AB=1,BF=1,
∴AF=
=
,同理CF=
,
在△ABC中,∵AB⊥BC,AB=BC=1,∴AC=
,
在△ACF中,∵AC=AF=CF,∴∠CAF=60°.
∴异面直线A1C1与B1D所成的角为60°.
(Ⅲ)解:∵直三棱柱ABC-A1B1C1,∴B1B⊥BC,
又AB⊥BC,AB∩BB1=B,∴BC⊥平面ABB1D.
如图,连接BD,
在△BB1D中,∵BD=B1D=
, BB1=2,
∴BD2+B1D2=BB12,即BD⊥B1D,
∵BD是CD在平面ABB1D内的射影,
∴CD⊥B1D,∴∠CDB为二面角C-B1D-B的平面角.
在△BCD中,∠CBD=90°,BC=1,BD=
,
∴tan∠CDB=
=
,∴二面角C-B1D-B的大小为arctan
.

在△BCB1中,∵BG=GC,B1E=EC,∴EG∥BB1,且EG=
| 1 |
| 2 |
又AD∥BB1,且AD=
| 1 |
| 2 |
∴四边形ADEG为平行四边形,∴DE∥AG,
又AG?平面ABC,DE?平面ABC,∴DE∥平面ABC.
(Ⅱ)解:如图,设F为BB1的中点,连接AF,CF,
∵直三棱柱ABC-A1B1C1,且D是AA1的中点,
∴AF∥B1D,A1C1∥AC,∴∠CAF为异面直线A1C1与B1D所成的角或其补角.
在Rt△ABF中,BF⊥AB,AB=1,BF=1,
∴AF=
| AB2+BF2 |
| 2 |
| 2 |
在△ABC中,∵AB⊥BC,AB=BC=1,∴AC=
| 2 |
在△ACF中,∵AC=AF=CF,∴∠CAF=60°.
∴异面直线A1C1与B1D所成的角为60°.
(Ⅲ)解:∵直三棱柱ABC-A1B1C1,∴B1B⊥BC,
又AB⊥BC,AB∩BB1=B,∴BC⊥平面ABB1D.
如图,连接BD,
在△BB1D中,∵BD=B1D=
| 2 |
∴BD2+B1D2=BB12,即BD⊥B1D,
∵BD是CD在平面ABB1D内的射影,
∴CD⊥B1D,∴∠CDB为二面角C-B1D-B的平面角.
在△BCD中,∠CBD=90°,BC=1,BD=
| 2 |
∴tan∠CDB=
| BC |
| BD |
| ||
| 2 |
| ||
| 2 |
点评:判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b?a∥α);③利用面面平行的性质定理(α∥β,a?α?a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α??a∥β).
求二面角,关键是构造出二面角的平面角,常用的方法有利用三垂线定理和通过求法向量的夹角,然后再将其转化为二面角的平面角.
求二面角,关键是构造出二面角的平面角,常用的方法有利用三垂线定理和通过求法向量的夹角,然后再将其转化为二面角的平面角.

练习册系列答案
相关题目




