题目内容
如图，在直三棱柱ABC-A1B1C1中，AB⊥BC，P为A1C1的中点，AB=BC=kPA．（I）求三棱锥P-AB1C与三棱锥C1-AB1P的体积之比；
（II）当k为何值时，直线PA⊥B1C．
分析：（I）B1P是三棱锥B1-PAC的高，B1P是三棱锥B1-PAC的高，
利用VP-AB1C=VB1-PAC=
•S△PAC•B1P以及
VC1-AB1P=VA-B1PC1=
•S△B1PC1•AA1求三棱锥P-AB1C与三棱锥C1-AB1P的体积之比；
（II）证明k=1，AP⊥面B1PC，推出直线PA⊥B1C．
利用VP-AB1C=VB1-PAC=
| 1 |
| 3 |
VC1-AB1P=VA-B1PC1=
| 1 |
| 3 |
（II）证明k=1，AP⊥面B1PC，推出直线PA⊥B1C．
解答：解：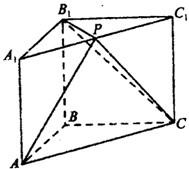
（I）由B1P⊥面A1C，
得B1P是三棱锥B1-PAC的高，
又∵AA1⊥面A1B1C1，∴AA1是三棱锥A-B1PC1的高．VP-AB1C=VB1-PAC=
•S△PAC•B1P（2分）VC1-AB1P=VA-B1PC1=
•S△B1PC1•AA1（4分）
=
=
=2，
所以三棱锥P-AB1C与三棱锥C1-AB1P的体积之比是2．（6分）
（II）要使直线AP⊥B1C，
只需AP⊥面B1PC．
因为B1P⊥面A1C，
所以B1P⊥AP．
所以只需PA⊥PC．（9分）∵PA=PC，所以只需PA=
AC，
又AC=
AB，AB=BC=kPA，∴k=1．（11分）
反知，当k=1时，AP⊥面B1PC，
所以AP⊥B1C成立．（11分）
（I）由B1P⊥面A1C，
得B1P是三棱锥B1-PAC的高，
又∵AA1⊥面A1B1C1，∴AA1是三棱锥A-B1PC1的高．VP-AB1C=VB1-PAC=
| 1 |
| 3 |
| 1 |
| 3 |
| VP-AB1C |
| VC1-AB1P |
| ||
|
| AC |
| PC1 |
所以三棱锥P-AB1C与三棱锥C1-AB1P的体积之比是2．（6分）
（II）要使直线AP⊥B1C，
只需AP⊥面B1PC．
因为B1P⊥面A1C，
所以B1P⊥AP．
所以只需PA⊥PC．（9分）∵PA=PC，所以只需PA=
| 2 |
又AC=
| 2 |
反知，当k=1时，AP⊥面B1PC，
所以AP⊥B1C成立．（11分）
点评：本题考查棱柱、棱锥、棱台的体积，空间中直线与直线之间的位置关系，考查空间想象能力，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
