摘要：解: 设 .则原方程可化为 ---2分 解得 ---4分 当时 解得 ---6分 当时 解得 ---8分 经检验原方程的解为. ---9分 方程两边都乘以得: ---3分 化简得: ---5分 解得 . ---8分 经检验原方程的解为. ---9分
网址：http://m.1010jiajiao.com/timu3_id_439000[举报]
为解方程(x2－1)2－5(x2－1)＋4=0，我们可以将x2－1视为一个整体，然后设x2－1=y，则y2=(x2－1)2，原方程化为y2－5y＋4=0，解此方程，得y1=1，y2=4。
当y=1时，x2－1=1，x2=2，∴x=±
。
当y=4时，x2－1=4，x2=5，∴x=±
。
∴原方程的解为x1=－
，x2=
，x3=－
，x4=
。
以上方法就叫换元法，达到了降次的目的，体现了转化的思想。
（1）运用上述方法解方程：x4－3x2－4=0。
（2）既然可以将x2－1看作一个整体，你能直接运用因式分解法解这个方程吗？
查看习题详情和答案>>
阅读理解：
计算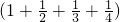
×
-
×
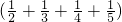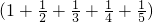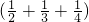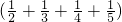时，若把与（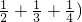
分别各看着一个整体，再利用分配律进行运算，可以大大简化难度．过程如下：
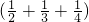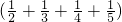解：设为A，为B，
则原式=B（1+A）-A（1+B）=B+AB-A-AB=B-A=
．请用上面方法计算：
①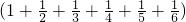
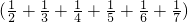
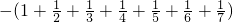
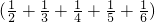
②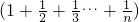
．
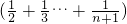
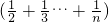查看习题详情和答案>>
阅读理解：
计算(1+
+
+
)×(
+
+
+
)-(1+
+
+
+
)×(
+
+
)时，若把(
+
+
+
)与（
+
+
)分别各看着一个整体，再利用分配律进行运算，可以大大简化难度．过程如下：
解：设(
+
+
)为A，(
+
+
+
)为B，
则原式=B（1+A）-A（1+B）=B+AB-A-AB=B-A=
．请用上面方法计算：
①(1+
+
+
+
+
)(
+
+
+
+
+
)-(1+
+
+
+
+
+
)(
+
+
+
+
)
②(1+
+
…+
)(
+
…+
)-(1+
+
…+
)(
+
…+
)．
查看习题详情和答案>>
计算(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
解：设(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
则原式=B（1+A）-A（1+B）=B+AB-A-AB=B-A=
| 1 |
| 5 |
①(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
②(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
阅读理解：
计算(1+
+
+
)×(
+
+
+
)-(1+
+
+
+
)×(
+
+
)时，若把(
+
+
+
)与（
+
+
)分别各看着一个整体，再利用分配律进行运算，可以大大简化难度．过程如下：
解：设(
+
+
)为A，(
+
+
+
)为B，
则原式=B（1+A）-A（1+B）=B+AB-A-AB=B-A=
．请用上面方法计算：
①(1+
+
+
+
+
)(
+
+
+
+
+
)-(1+
+
+
+
+
+
)(
+
+
+
+
)
②(1+
+
…+
)(
+
…+
)-(1+
+
…+
)(
+
…+
)．
查看习题详情和答案>>
计算(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
解：设(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
则原式=B（1+A）-A（1+B）=B+AB-A-AB=B-A=
| 1 |
| 5 |
①(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
②(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| |||||||||||||||||||||||||||||||||||||||||
．
，则原方程可以化为y2－5y＋6＝0．